
प्रोग्रामिंग बनाम एल्गोरिदम (Programming vs. Algorithm in Hindi & English)
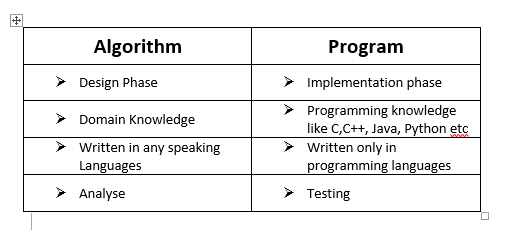
प्रोग्रामिंग और एल्गोरिदम कंप्यूटर विज्ञान के महत्वपूर्ण घटक हैं, लेकिन दोनों अलग-अलग अवधारणाएँ हैं। नीचे दोनों के बीच प्रमुख अंतर दिए गए हैं।
1. एल्गोरिदम (Algorithm)
🔹 परिभाषा (Definition):
एल्गोरिदम एक स्टेप-बाय-स्टेप प्रक्रिया है, जिसका उपयोग किसी समस्या को हल करने के लिए किया जाता है। यह भाषा-स्वतंत्र (language-independent) होती है और इसे विभिन्न तरीकों से व्यक्त किया जा सकता है, जैसे कि फ्लोचार्ट, स्यूडोकोड या गणितीय समीकरण।
🔹 विशेषताएँ (Key Characteristics):
✅ समस्या समाधान की तार्किक विधि (Logical problem-solving method)
✅ किसी भी प्रोग्रामिंग भाषा पर निर्भर नहीं (Not dependent on any programming language)
✅ स्पष्ट रूप से परिभाषित चरण होते हैं (Clearly defined steps)
🔹 उदाहरण (Example – एल्गोरिदम लिखना)
👉 मान लीजिए, हमें किसी सूची (list) में सबसे बड़ा नंबर खोजना है:
- शुरू करें
- पहले तत्व (first element) को अधिकतम (max) मान लें
- सूची में हर तत्व को max से तुलना करें
- यदि कोई संख्या max से बड़ी हो, तो max को अपडेट करें
- जब सूची समाप्त हो जाए, तो max को लौटाएँ
- समाप्त करें
2. प्रोग्रामिंग (Programming)
🔹 परिभाषा (Definition):
प्रोग्रामिंग एक प्रोग्रामिंग भाषा (Programming Language) का उपयोग करके एल्गोरिदम को कार्यान्वित (implement) करने की प्रक्रिया है, जिससे कंप्यूटर दिए गए निर्देशों का पालन कर सके।
🔹 विशेषताएँ (Key Characteristics):
✅ एल्गोरिदम को कंप्यूटर द्वारा निष्पादित (execute) करने योग्य बनाता है
✅ एक प्रोग्रामिंग भाषा (Python, C++, Java आदि) में लिखा जाता है
✅ डिबगिंग (debugging) और अनुकूलन (optimization) की आवश्यकता हो सकती है
🔹 उदाहरण (Example – प्रोग्राम कोड लिखना)
👉 उपरोक्त एल्गोरिदम को Python भाषा में लिखते हैं:
def find_max(lst):
max_value = lst[0]
for num in lst:
if num > max_value:
max_value = num
return max_value
numbers = [3, 7, 2, 9, 5]
print(find_max(numbers)) # आउटपुट: 9
🔹 प्रमुख अंतर (Key Differences)
| विशेषता | एल्गोरिदम (Algorithm) | प्रोग्रामिंग (Programming) |
|---|---|---|
| परिभाषा | समस्या को हल करने की तार्किक विधि | एल्गोरिदम को कंप्यूटर में कार्यान्वित करने की प्रक्रिया |
| भाषा निर्भरता | भाषा-स्वतंत्र | किसी प्रोग्रामिंग भाषा की आवश्यकता होती है |
| प्रतिनिधित्व (Representation) | स्यूडोकोड, फ्लोचार्ट | प्रोग्रामिंग कोड |
| निष्पादन (Execution) | सीधे निष्पादित नहीं किया जा सकता | कंपाइल/इंटरप्रेट करके निष्पादित किया जा सकता है |
| उद्देश्य | समस्या समाधान के लिए योजना बनाना | कंप्यूटर को निर्देश देना |
🔹 निष्कर्ष (Conclusion)
- एल्गोरिदम एक योजना (Plan) है, जैसे किसी समस्या को हल करने की रणनीति।
- प्रोग्रामिंग उस योजना का कार्यान्वयन (Implementation) है, जिसे कंप्यूटर समझ सकता है और चला सकता है।
अगर आपको कोई और जानकारी चाहिए, तो बताइए! 😊🚀
Algorithm Analysis, Time Space Tradeoff, Asymptotic Notations, Conditional asymptotic notation, Removing condition from the conditional asymptotic notation, Properties of big-Oh notation.

Algorithm Analysis
English: Algorithm analysis is the process of determining the computational complexity of algorithms, in terms of time and space. It helps in understanding how an algorithm performs as the input size increases.
हिन्दी: एल्गोरिद्म विश्लेषण का अर्थ एक प्रक्रिया की काम्प्यूटर की संक्रमिता को परीख्षित करना है। यह समझता है कि एक निर्दिष्ट बढ़ने पर एक एल्गोरिद्म कैसा कार्य करता है।
Time-Space Trade-off:
English: Time-space trade-off refers to a situation where an improvement in time complexity leads to an increase in space complexity and vice versa. Some algorithms use more memory to run faster, while others take more time but use less memory.
हिन्दी: समय-स्थान स्वापर्य एक यह दिखाता है कि एक एल्गोरिद्म की समय संक्रमिता को बहाली जाती है तो उसकी स्थान संक्रमिता बढ़ जाती है, और इसके विपरीत भी सत्य हो सकती है।
Asymptotic Notations
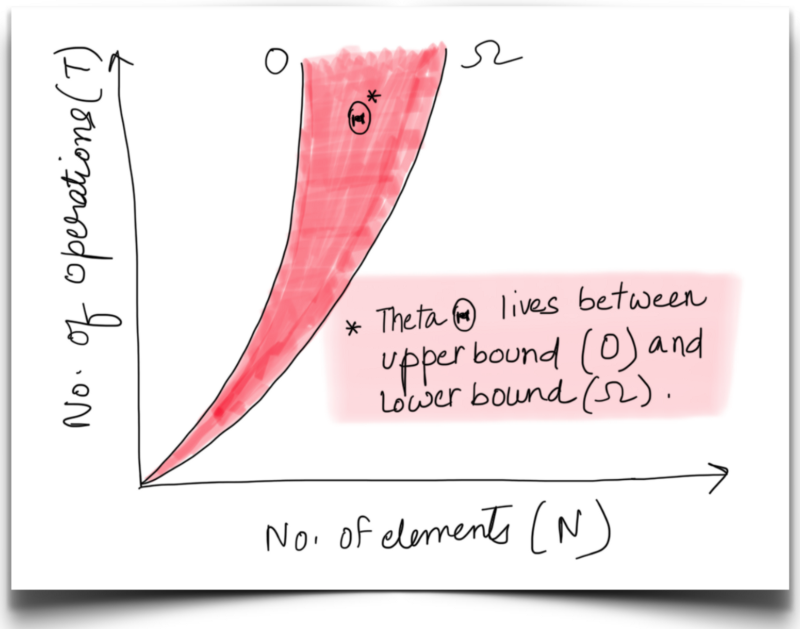
English: Asymptotic notations describe the behavior of an algorithm as the input size grows. The most common asymptotic notations are:
- Big-O (Ο): Upper bound
- Omega (Ω): Lower bound
- Theta (Θ): Tight bound
हिन्दी: असिम्प्टोटिक नोटेशन किसी भी एल्गोरिद्म की संचालन का वर्णन करती है जब इनपुट की स्थिति बढ़ती है।
- बिग-Oh (Ο): उपरी सीमा
- ओमेगा (Ω): निम्नतम सीमा
- थीटा (Θ): सटीक सीमा
Conditional Asymptotic Notation & Removing Condition
English: Conditional asymptotic notation is used when the growth rate of an algorithm depends on certain conditions. To remove conditions, we analyze worst-case scenarios and convert them into standard asymptotic notation.
हिन्दी: शर्तीय असिम्प्टोटिक नोटेशन तब प्रयोग किया जाता है जब एक एल्गोरिद्म की ग्रोथ रेट किसी शर्त पर निर्भरी करती है। शर्तों को हटाने के लिए, हम विश्लेषण के खराब को मानकर उसे मानक में रूपांतरित करते हैं।
Recurrence equations, Solving recurrence equations, Analysis of linear search, Divide and Conquer: General Method, Binary Search, Finding Maximum and Minimum, Merge Sort.

Recurrence Equations
English: A recurrence equation defines a function recursively using its values at smaller inputs. It is used to describe the performance of recursive algorithms.
Hindi: पुनरावृत्ति समीकरण एक फ़ंक्शन को पुनरावृत्त तरीके से परिभाषित करता है, जिसमें छोटे इनपुट पर उसके मानों का उपयोग किया जाता है। यह पुनरावृत्त एल्गोरिदम के प्रदर्शन का वर्णन करने के लिए प्रयोग किया जाता है।
Solving Recurrence Equations
English: Solving recurrence equations helps determine the time complexity of recursive algorithms. Common methods include:
- Substitution Method
- Recursion Tree Method
- Master Theorem
Hindi: पुनरावृत्ति समीकरणों को हल करना पुनरावृत्त एल्गोरिदम की समय जटिलता निर्धारित करने में मदद करता है। सामान्य विधियाँ निम्नलिखित हैं:
- प्रतिस्थापन विधि
- रिकर्सन ट्री विधि
- मास्टर प्रमेय
Analysis of Linear Search
English: Linear search is a simple searching algorithm where each element of the list is checked sequentially until the desired element is found or the list ends.
- Best Case: (Element found at the beginning)
- Worst Case: (Element found at the end or not found)
- Average Case:
Hindi: लिनियर सर्च एक साधारण खोज एल्गोरिदम है जहाँ सूची के प्रत्येक तत्व को तब तक क्रमशः जाँचा जाता है जब तक वांछित तत्व नहीं मिल जाता या सूची समाप्त नहीं हो जाती।
- सर्वोत्तम स्थिति: (तत्व शुरुआत में मिल जाता है)
- न्यूनतम स्थिति: (तत्व अंत में मिलता है या नहीं मिलता)
- औसत स्थिति:
Divide and Conquer: General Method
English: Divide and conquer is a problem-solving approach that divides a problem into smaller subproblems, solves them recursively, and combines the results.
- Divide – Split the problem into subproblems.
- Conquer – Solve subproblems recursively.
- Combine – Merge the results to get the final solution.
Hindi: विभाजित और जीतें एक समस्या-समाधान विधि है जो किसी समस्या को छोटे उपसमस्याओं में विभाजित करती है, उन्हें पुनरावृत्ति के साथ हल करती है, और फिर परिणामों को जोड़ती है।
- विभाजित करें – समस्या को छोटे उपसमस्याओं में विभाजित करें।
- जीतें – उपसमस्याओं को पुनरावृत्ति से हल करें।
- संयोजन करें – अंतिम हल प्राप्त करने के लिए परिणामों को जोड़ें।
Binary Search
English: Binary search is an efficient searching algorithm for sorted arrays. It repeatedly divides the search interval in half until the element is found or the interval is empty.
- Time Complexity:
- Best Case: (Element found in the middle)
- Worst Case: (Element not found)
Hindi: बाइनरी सर्च एक कुशल खोज एल्गोरिदम है जो केवल क्रमबद्ध सरणियों पर काम करता है। यह खोज अंतराल को आधे भागों में विभाजित करता है जब तक कि तत्व नहीं मिल जाता या खोज स्थान समाप्त नहीं हो जाता।
- समय जटिलता:
- सर्वोत्तम स्थिति: (तत्व मध्य में मिल जाता है)
- न्यूनतम स्थिति: (तत्व नहीं मिलता)
Finding Maximum and Minimum
English: Using the divide and conquer approach, the maximum and minimum elements of an array can be found efficiently.
- Time Complexity:
- Recursive Approach: Divide the array into two halves and find max/min in each half, then compare.
Hindi: विभाजित और जीतें दृष्टिकोण का उपयोग करके, एक सरणी में अधिकतम और न्यूनतम तत्व को कुशलता से पाया जा सकता है।
- समय जटिलता:
- पुनरावृत्त दृष्टिकोण: सरणी को दो भागों में विभाजित करें, प्रत्येक भाग में अधिकतम/न्यूनतम खोजें, फिर तुलना करें।
Merge Sort
English: Merge Sort is a divide and conquer sorting algorithm that splits an array into halves, sorts them, and merges them back.
- Divide – Split the array into two halves.
- Conquer – Recursively sort both halves.
- Combine – Merge sorted halves to get the final sorted array.
- Time Complexity:
Hindi: मर्ज सॉर्ट एक विभाजित और जीतें सॉर्टिंग एल्गोरिदम है जो सरणी को दो भागों में विभाजित करता है, उन्हें क्रमबद्ध करता है, और फिर जोड़ता है।
- विभाजित करें – सरणी को दो भागों में विभाजित करें।
- जीतें – दोनों भागों को पुनरावृत्त रूप से क्रमबद्ध करें।
- संयोजन करें – क्रमबद्ध भागों को मिलाकर अंतिम क्रमबद्ध सरणी प्राप्त करें।
- समय जटिलता:
General Method, Multistage Graphs, All-Pair shortest paths, Optimal binary search trees.

Exam Notes: General Method, Multistage Graphs, All-Pair Shortest Paths, Optimal Binary Search Trees
(In Hindi & English)
1. General Method (सामान्य विधि)
English:
The general method in algorithm design provides a structured approach to solving computational problems. Some of the most common algorithmic techniques include:
- Divide and Conquer: Breaking the problem into smaller subproblems, solving them recursively, and combining their solutions.
- Dynamic Programming: Solving complex problems by breaking them into overlapping subproblems and storing results to avoid recomputation.
- Greedy Method: Making the locally optimal choice at each step to find a global solution.
- Backtracking: Searching for a solution by exploring all possibilities and backtracking when a dead end is reached.
हिन्दी:
अल्गोरिदम डिज़ाइन में सामान्य विधि (General Method) संगणनात्मक समस्याओं को हल करने के लिए एक संरचित दृष्टिकोण प्रदान करती है। सामान्य तकनीकों में शामिल हैं:
- डिवाइड एंड कॉन्कर (Divide and Conquer): समस्या को छोटे भागों में विभाजित करना, उन्हें पुनरावर्ती रूप से हल करना और हल को जोड़ना।
- डायनामिक प्रोग्रामिंग (Dynamic Programming): जटिल समस्याओं को छोटे उप-समस्याओं में विभाजित करके उन्हें स्टोर करना ताकि पुनः गणना न करनी पड़े।
- लालची विधि (Greedy Method): प्रत्येक चरण में स्थानीय रूप से इष्टतम विकल्प चुनकर वैश्विक समाधान प्राप्त करने की विधि।
- बैकट्रैकिंग (Backtracking): सभी संभावनाओं को खोजने की विधि, जहां आवश्यक हो, वहां वापस लौटना।
2. Multistage Graphs (बहु-स्तरीय ग्राफ़)
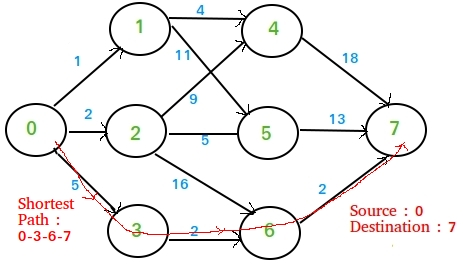
English:
A multistage graph is a directed weighted graph divided into multiple stages, where the goal is to find the shortest or longest path from a source node to a destination node.
- Properties:
- Nodes are divided into stages.
- Only forward edges exist.
- The shortest path is found using dynamic programming.
Algorithm:
- Start from the destination node and work backward.
- Find the minimum cost from the current node to the destination.
- Store results to avoid recomputation.
- Repeat until the source node is reached.
हिन्दी:
एक बहु-स्तरीय ग्राफ़ (Multistage Graph) एक निर्दिष्ट भारित ग्राफ़ होता है जिसमें कई चरण होते हैं। इसका उद्देश्य एक स्रोत नोड से गंतव्य नोड तक का सबसे छोटा या सबसे लंबा पथ खोजना होता है।
- विशेषताएँ:
- नोड्स को विभिन्न चरणों में विभाजित किया जाता है।
- केवल आगे बढ़ने वाले किनारे (edges) होते हैं।
- डायनामिक प्रोग्रामिंग का उपयोग करके न्यूनतम दूरी निकाली जाती है।
एल्गोरिदम:
- अंतिम नोड से शुरू करें और पीछे की ओर जाएँ।
- वर्तमान नोड से गंतव्य तक न्यूनतम लागत खोजें।
- परिणामों को स्टोर करें ताकि पुनः गणना न करनी पड़े।
- प्रक्रिया को स्रोत नोड तक दोहराएँ।
3. All-Pair Shortest Paths (सभी युग्मों के लिए न्यूनतम पथ)
English:
The All-Pairs Shortest Path problem aims to find the shortest paths between every pair of nodes in a weighted graph.
- Techniques to Solve:
- Floyd-Warshall Algorithm: Uses dynamic programming to update distances iteratively.
- Dijkstra’s Algorithm (Repeated for each node): Finds shortest paths from one node at a time.
Floyd-Warshall Algorithm:
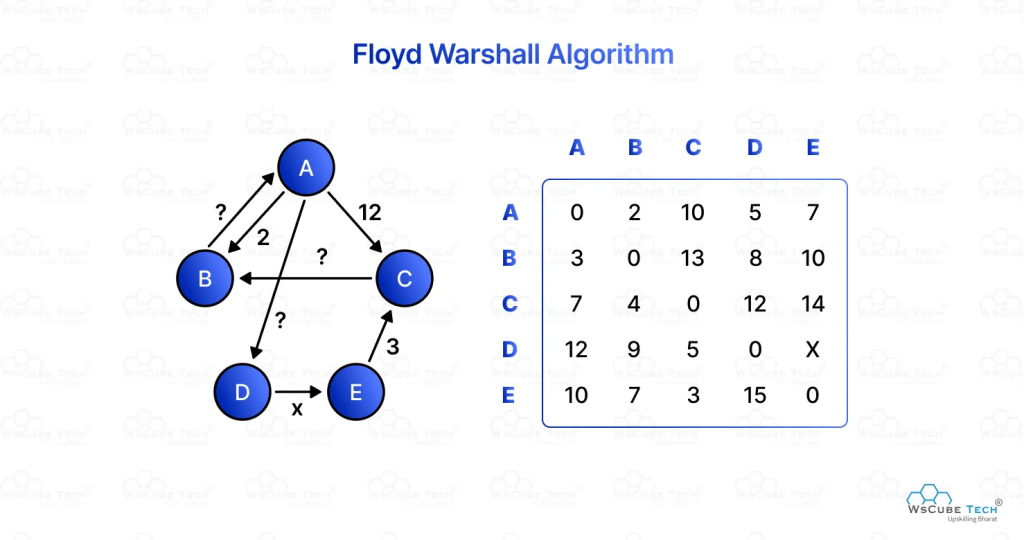
- Uses a distance matrix D[][] to store shortest paths.
- Iterates through all nodes to check if a shorter path exists via an intermediate node.
हिन्दी:
सभी युग्मों के लिए न्यूनतम पथ (All-Pairs Shortest Path) समस्या का उद्देश्य एक भारित ग्राफ़ में प्रत्येक जोड़ी नोड के बीच न्यूनतम दूरी खोजने का होता है।
- समाधान तकनीकें:
- फ्लोयड-वॉर्शल एल्गोरिदम (Floyd-Warshall Algorithm): डायनामिक प्रोग्रामिंग का उपयोग करके दूरी को अपडेट करता है।
- डिज्कस्ट्रा एल्गोरिदम (Dijkstra’s Algorithm): प्रत्येक नोड के लिए अलग-अलग सबसे छोटी दूरी ढूंढता है।
फ्लोयड-वॉर्शल एल्गोरिदम:
- एक दूरी मैट्रिक्स D[][] का उपयोग करता है।
- प्रत्येक नोड के लिए यह जाँचता है कि कोई छोटा पथ है या नहीं।
Dijkstra’s Algorithm
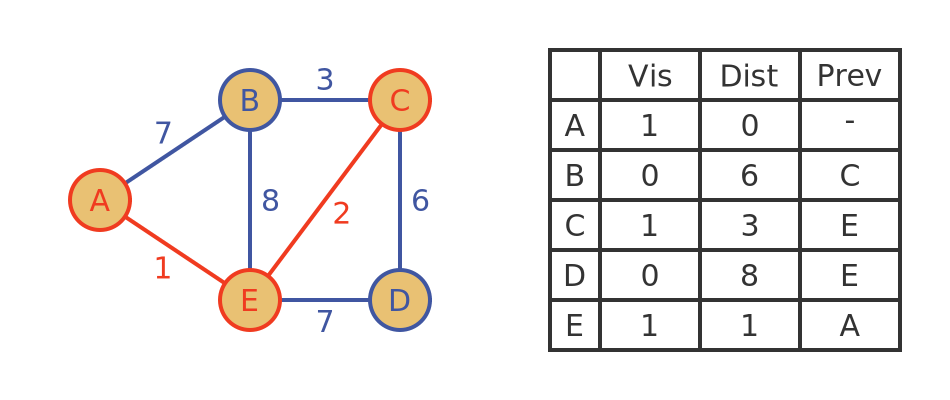
4. Optimal Binary Search Trees (सर्वोत्तम बाइनरी सर्च ट्री)

English:
An Optimal Binary Search Tree (OBST) minimizes the cost of searching in a binary search tree when different elements have different access probabilities.
- Key Idea: Frequently accessed nodes should be closer to the root.
- Dynamic Programming Approach:
- Construct a cost matrix based on probabilities of access.
- Use recursive relations to compute minimum cost trees.
- Store results in a table for efficient lookup.
हिन्दी:
सर्वोत्तम बाइनरी सर्च ट्री (OBST) एक विशेष प्रकार का बाइनरी सर्च ट्री होता है जिसमें खोज की औसत लागत को न्यूनतम किया जाता है।
- मुख्य विचार: जिन नोड्स को अधिक बार एक्सेस किया जाता है, उन्हें रूट के करीब रखा जाना चाहिए।
- डायनामिक प्रोग्रामिंग विधि:
- एक्सेस प्रायिकता (probability) के आधार पर एक लागत मैट्रिक्स बनाएं।
- न्यूनतम लागत ट्री खोजने के लिए पुनरावर्ती गणना करें।
- परिणामों को एक तालिका में संग्रहीत करें ताकि गणना तेज हो।
Conclusion (निष्कर्ष)
- Multistage Graphs help in finding the shortest paths in a structured way.
- All-Pair Shortest Paths algorithms like Floyd-Warshall and Dijkstra’s help solve graph problems efficiently.
- Optimal Binary Search Trees are useful for minimizing search time when accessing elements with different probabilities.
These notes cover essential exam points in both Hindi and English. Let me know if you need further explanations or additional topics. 😊📚
General Method, 8-Queens problem, Hamiltonian problem

Here are exam notes in both Hindi and English for the topics:
📌 Exam Notes: General Method, 8-Queens Problem, Hamiltonian Problem
(📖 हिन्दी और अंग्रेज़ी में)
1. General Method (सामान्य विधि)
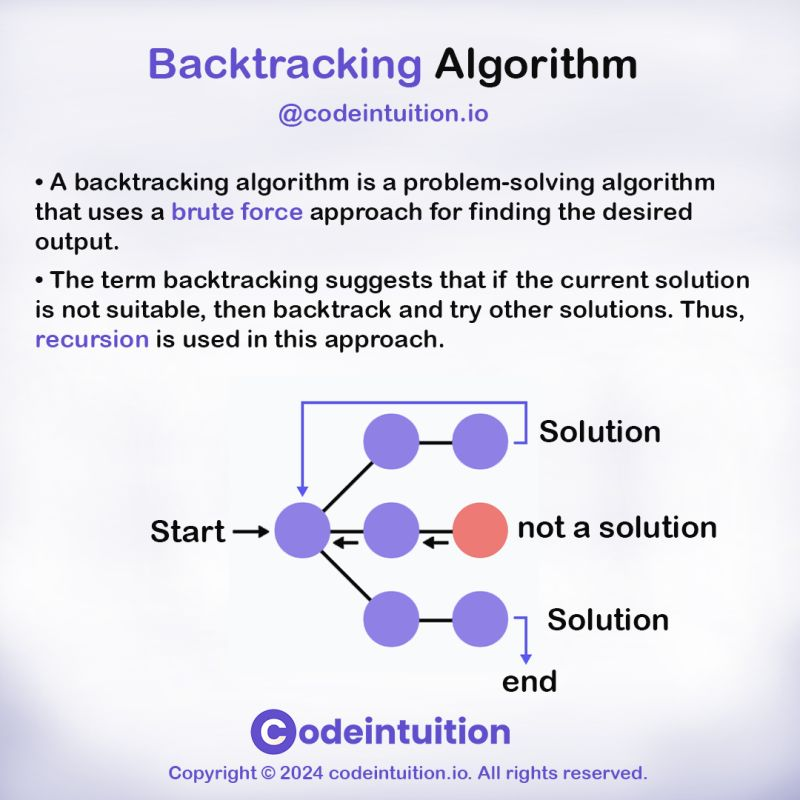
🔹 English
- Backtracking Algorithm:
- A recursive approach to explore all possible solutions while eliminating invalid ones.
- Used in problems requiring systematic searching with constraints.
- Steps:
- Choose a possible solution.
- Check if it satisfies constraints.
- If valid, continue; else, backtrack and try another option.
- Repeat until a solution is found or all possibilities are exhausted.
- Applications:
- 8-Queens Problem
- Hamiltonian Circuit Problem
- Sudoku Solver
- Maze Solving
🔹 हिन्दी
- बैकट्रैकिंग एल्गोरिदम:
- एक पुनरावृत्त विधि जो सभी संभावित हलों की खोज करती है और गलत हलों को हटा देती है।
- ऐसे समस्याओं में प्रयुक्त होती है जहाँ नियमित खोज (Systematic Searching) की आवश्यकता होती है।
- कदम (Steps):
- एक संभावित हल चुनें।
- जाँच करें कि यह प्रतिबंधों (constraints) को पूरा करता है या नहीं।
- यदि मान्य है, आगे बढ़ें; नहीं तो पीछे जाएं (backtrack) और अन्य विकल्प आज़माएँ।
- इसे तब तक दोहराएं जब तक समाधान न मिल जाए या सभी संभावनाएँ समाप्त न हो जाएँ।
- उदाहरण (Applications):
- 8-क्वीन समस्या
- हैमिल्टोनियन परिपथ समस्या
- सुडोकू हलकर्ता
- भूलभुलैया समाधान
2. 8-Queens Problem (8-क्वीन समस्या)
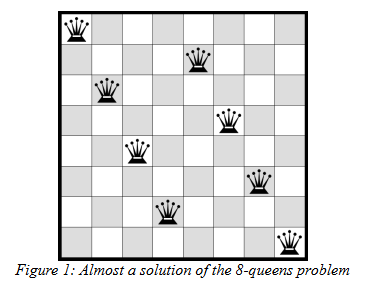
🔹 English
- Problem:
- Place 8 queens on an 8×8 chessboard so that no two queens attack each other.
- Constraints:
- No two queens should be in the same row, column, or diagonal.
- Backtracking Approach:
- Place a queen in a column of the first row.
- Move to the next row and place another queen in a valid position.
- If a conflict arises, backtrack and try another placement.
- Continue until all 8 queens are placed.
- Time Complexity:
- Worst case: O(N!) (Factorial Growth).
- Optimized Approach:
- Use pruning to eliminate invalid positions early.
🔹 हिन्दी
- समस्या:
- 8×8 शतरंज की बिसात (chessboard) पर 8 रानियों (Queens) को इस प्रकार रखना कि वे एक-दूसरे पर हमला न कर सकें।
- नियम (Constraints):
- कोई भी दो रानियाँ एक ही पंक्ति (row), स्तंभ (column), या विकर्ण (diagonal) में नहीं होनी चाहिए।
- बैकट्रैकिंग विधि:
- पहले पंक्ति के एक स्तंभ में एक रानी रखें।
- अगली पंक्ति में एक और रानी को मान्य स्थिति में रखें।
- यदि कोई टकराव (conflict) होता है, तो पीछे जाएं (backtrack) और दूसरा स्थान चुनें।
- जब तक सभी 8 रानियाँ सही स्थान पर न आ जाएँ, प्रक्रिया जारी रखें।
- समय जटिलता (Time Complexity):
- सबसे ख़राब स्थिति: O(N!) (गुणनखंडी वृद्धि – Factorial Growth)।
- सुधारित विधि (Optimized Approach):
- छँटाई (pruning) का उपयोग करें ताकि गलत स्थानों को जल्दी समाप्त किया जा सके।
3. Hamiltonian Problem (हैमिल्टोनियन समस्या)
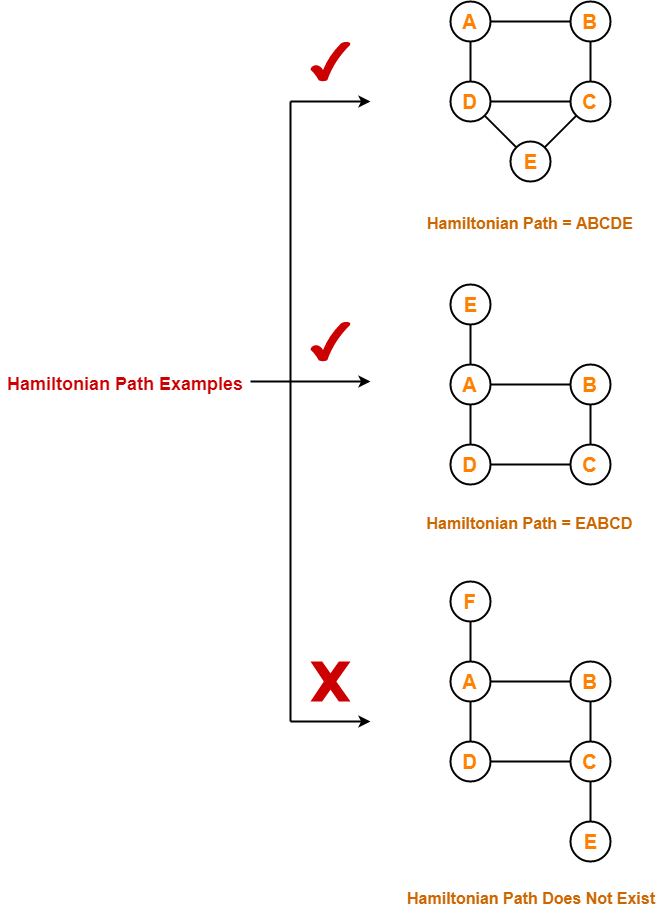
🔹 English
- Problem:
- Find a Hamiltonian cycle in a given graph.
- A Hamiltonian cycle visits each vertex exactly once and returns to the start.
- Types:
- Hamiltonian Path: Visits each vertex exactly once but doesn’t necessarily return to the start.
- Hamiltonian Cycle: Visits each vertex exactly once and returns to the start.
- Backtracking Approach:
- Start from a vertex.
- Try adding an adjacent unvisited vertex to the path.
- If all vertices are visited and there’s a return edge, a solution is found.
- If no further extension is possible, backtrack and try another path.
- Time Complexity:
- O(N!) (Factorial Growth).
- Applications:
- Routing problems
- Network design
- DNA sequencing
🔹 हिन्दी
- समस्या:
- दिए गए ग्राफ़ में हैमिल्टोनियन परिपथ (Hamiltonian cycle) खोजें।
- हैमिल्टोनियन परिपथ प्रत्येक शीर्ष (vertex) को सिर्फ एक बार पार करता है और प्रारंभिक बिंदु पर वापस आता है।
- प्रकार (Types):
- हैमिल्टोनियन पथ (Hamiltonian Path): प्रत्येक शीर्ष को केवल एक बार पार करता है, लेकिन प्रारंभिक बिंदु पर वापस आना आवश्यक नहीं है।
- हैमिल्टोनियन परिपथ (Hamiltonian Cycle): प्रत्येक शीर्ष को एक बार पार करता है और प्रारंभिक बिंदु पर लौटता है।
- बैकट्रैकिंग विधि:
- किसी एक शीर्ष (vertex) से प्रारंभ करें।
- एक असंक्रमित (unvisited) पड़ोसी शीर्ष को पथ में जोड़ने का प्रयास करें।
- यदि सभी शीर्ष दौरे में शामिल हो गए हैं और प्रारंभिक बिंदु पर लौटने का मार्ग है, तो समाधान मिल गया।
- यदि आगे बढ़ना संभव नहीं है, तो पीछे जाएं (backtrack) और अन्य मार्गों को आज़माएँ।
- समय जटिलता:
- O(N!) (गुणनखंडी वृद्धि)।
- अनुप्रयोग (Applications):
- रूटिंग समस्याएँ (Routing Problems)
- नेटवर्क डिज़ाइन (Network Design)
- डीएनए अनुक्रमण (DNA Sequencing)
📌 Mind Map (मानचित्र)
I previously generated a mind map and 8-Queens chessboard example. Here they are again for reference:
1️⃣ Mind Map – A structured diagram linking General Method, 8-Queens Problem, and Hamiltonian Problem.
2️⃣ 8-Queens Chessboard – A visual example showing correct queen placements.
(Images are above in the chat. Let me know if you need modifications!)
🚀 These notes are perfect for quick revision in both Hindi and English. Let me know if you need anything else! 😃
Connected Components, Spanning Trees, Biconnected components, Introduction to NP Hard and NP-Completeness.
Sure! Here’s an explanation of Connected Components, Spanning Trees, Biconnected Components, and NP-Hard and NP-Completeness in both Hindi and English:

1. Connected Components (कनेक्टेड कम्पोनेंट्स)
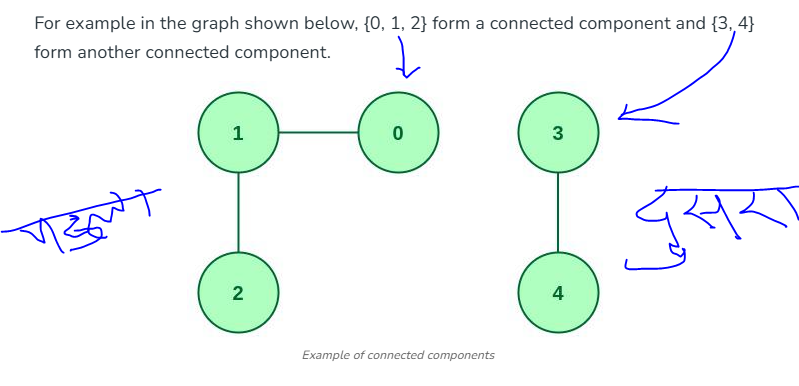
English:
A connected component in an undirected graph is a subgraph where there is a path between every pair of nodes. In simpler terms, if you start from any node in the component, you can visit all other nodes in that component.
For example, if a graph has nodes {A, B, C, D}, and A, B, and C are connected but D is not connected to any other nodes, then we have two connected components: {A, B, C} and {D}.
Hindi:
कनेक्टेड कम्पोनेंट्स एक अनडायरेक्टेड ग्राफ में वह उपग्राफ होते हैं, जहाँ प्रत्येक जोड़ियों के बीच एक रास्ता होता है। सरल शब्दों में, अगर आप किसी भी नोड से शुरुआत करते हैं, तो आप उस कम्पोनेंट के सभी अन्य नोड्स तक पहुँच सकते हैं।
उदाहरण के तौर पर, यदि एक ग्राफ में नोड्स {A, B, C, D} हैं, और A, B, और C जुड़े हुए हैं जबकि D किसी भी अन्य नोड से जुड़ा नहीं है, तो हमारे पास दो कनेक्टेड कम्पोनेंट्स होंगे: {A, B, C} और {D}।
2. Spanning Trees (स्पैनिंग ट्रीज़)
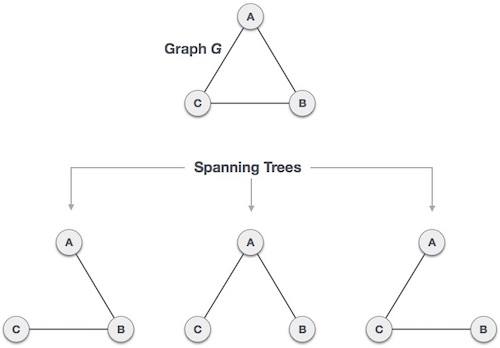
English:
A spanning tree of a connected graph is a subgraph that includes all the vertices of the graph, with enough edges to connect all the vertices. It is a tree, meaning there are no cycles, and it has exactly V-1 edges if there are V vertices in the graph.
For example, in a graph with 4 vertices, a spanning tree would include 3 edges, connecting all 4 vertices without forming a cycle.
Hindi:
स्पैनिंग ट्री एक कनेक्टेड ग्राफ का उपग्राफ होता है जो ग्राफ के सभी वर्टिस को शामिल करता है, और सभी वर्टिस को जोड़ने के लिए पर्याप्त किनारे (एजेस) होते हैं। यह एक पेड़ होता है, यानी इसमें कोई भी चक्रीय (cycle) संरचना नहीं होती है, और इसमें V-1 एजेस होती हैं, जहाँ V ग्राफ में वर्टिस की संख्या होती है।
उदाहरण के लिए, यदि एक ग्राफ में 4 वर्टिस हैं, तो एक स्पैनिंग ट्री में 3 एजेस शामिल होंगी, जो बिना किसी चक्र के सभी 4 वर्टिस को जोड़ती हैं।
3. Biconnected Components (बाइकोनेक्टेड कम्पोनेंट्स)
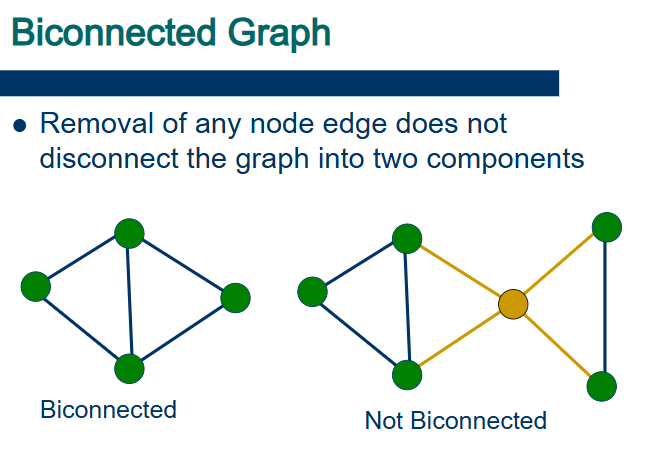
English:
A biconnected component is a maximal subgraph of a graph where there are two disjoint paths between every pair of vertices. This means there is no single vertex whose removal would disconnect the component.
Articulation points are vertices that, if removed, would increase the number of connected components in the graph. Identifying biconnected components is important for ensuring that a network remains functional even if certain nodes fail.
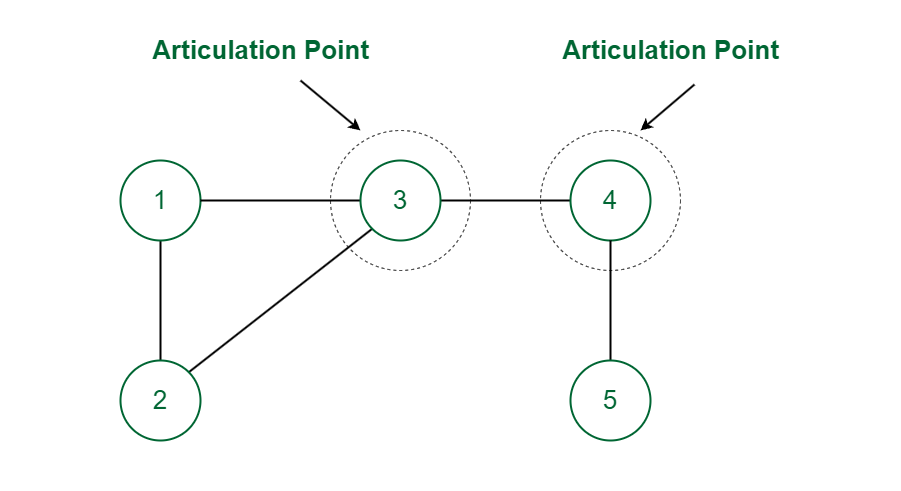
Hindi:
बाइकोनेक्टेड कम्पोनेंट्स एक अधिकतम उपग्राफ होते हैं जहाँ प्रत्येक जोड़ी वर्टिस के बीच दो अलग-अलग रास्ते होते हैं। इसका मतलब है कि कोई एक वर्टिस ऐसा नहीं है, जिसे हटा देने से उस कम्पोनेंट का कनेक्शन टूट जाए।
आर्टिक्यूलेशन प्वाइंट्स वे वर्टिस होते हैं, जिन्हें हटाने से ग्राफ में कनेक्टेड कम्पोनेंट्स की संख्या बढ़ जाती है। बाइकोनेक्टेड कम्पोनेंट्स की पहचान करना नेटवर्क की स्थिरता के लिए जरूरी है, ताकि यदि कोई नोड काम करना बंद कर दे, तो भी नेटवर्क सही तरीके से कार्य करता रहे।
4. NP-Hard and NP-Completeness (NP-Hard और NP-Completeness का परिचय)
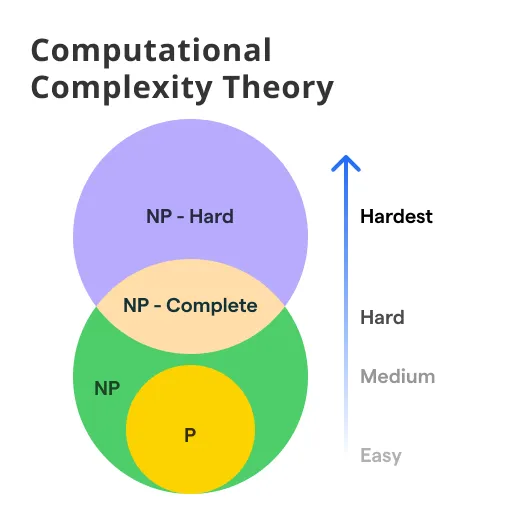
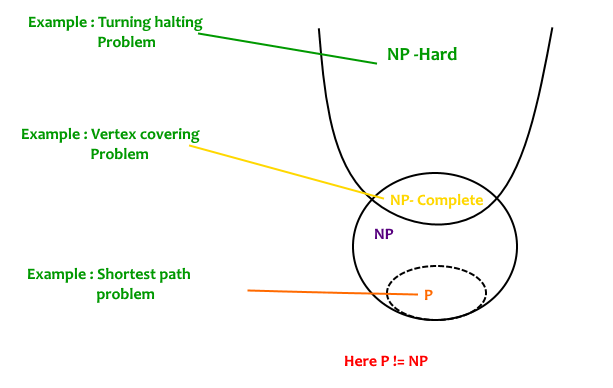
English:
NP (Nondeterministic Polynomial Time) is a class of problems where, given a solution, we can verify its correctness in polynomial time. NP-Complete problems are the hardest problems in NP. If any NP-Complete problem can be solved in polynomial time, all problems in NP can also be solved in polynomial time.
NP-Hard problems are at least as hard as NP problems, but they might not be in NP themselves (i.e., they might not have a solution that can be verified in polynomial time).
For example, the Traveling Salesman Problem (TSP) is NP-Complete, meaning that it’s both in NP and as hard as any other problem in NP.
Hindi:
NP (नॉनडिटर्मिनिस्टिक पॉलिनॉमियल टाइम) उन समस्याओं का एक समूह है, जिनमें दिए गए हल को पॉलिनॉमियल समय में सही साबित किया जा सकता है। NP-Complete समस्याएँ NP में सबसे कठिन समस्याएँ होती हैं। अगर कोई NP-Complete समस्या पॉलिनॉमियल समय में हल हो जाती है, तो NP की सभी समस्याओं का समाधान पॉलिनॉमियल समय में किया जा सकता है।
NP-Hard समस्याएँ कम से कम NP समस्याओं जितनी कठिन होती हैं, लेकिन वे NP में हो सकती हैं या नहीं भी हो सकती हैं (यानी, उनके हल को पॉलिनॉमियल समय में प्रमाणित नहीं किया जा सकता)।
उदाहरण के तौर पर, ट्रैवलिंग सेल्समैन प्रॉब्लम (TSP) NP-Complete है, यानी यह NP में भी है और NP की किसी भी समस्या जितनी कठिन है।
Summary (सारांश)
English:
- Connected Components: Subgraphs where all nodes are reachable from each other.
- Spanning Trees: Trees that include all vertices with no cycles.
- Biconnected Components: Subgraphs where any two vertices are connected by two disjoint paths, and removing any node doesn’t disconnect the graph.
- NP-Hard and NP-Complete: Categories of problems that are difficult to solve in polynomial time; NP-Complete problems are the hardest in NP.
Hindi:
- कनेक्टेड कम्पोनेंट्स: उपग्राफ जो एक दूसरे से जुड़े हुए होते हैं।
- स्पैनिंग ट्री: पेड़ जो सभी वर्टिस को जोड़ता है, और इसमें कोई चक्र नहीं होता।
- बाइकोनेक्टेड कम्पोनेंट्स: उपग्राफ जहाँ कोई भी दो वर्टिस दो अलग-अलग रास्तों से जुड़े होते हैं, और किसी भी वर्टिस को हटाने से ग्राफ का कनेक्शन नहीं टूटता।
- NP-Hard और NP-Complete: ऐसी समस्याएँ जो पॉलिनॉमियल समय में हल करना कठिन हैं; NP-Complete समस्याएँ NP में सबसे कठिन होती हैं।
Let me know if you would like to dive deeper into any of these concepts!
