Solving math problems quickly requires a combination of conceptual understanding, shortcuts, and practice. Here are some key strategies to improve speed and accuracy:
1. Master Basic Concepts
- Ensure you have strong fundamentals in arithmetic, algebra, geometry, and number properties.
- Learn formulas thoroughly (e.g., quadratic formula, percentage formulas, trigonometric identities).
2. Use Mental Math Tricks
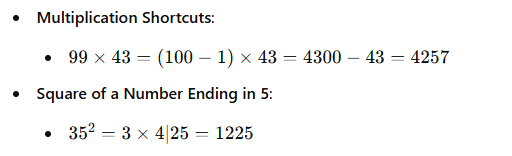
- Divisibility Rules:
- A number is divisible by 3 if the sum of its digits is divisible by 3
3. Approximation & Estimation
- Instead of exact calculations, round numbers for quick estimates (useful in competitive exams).
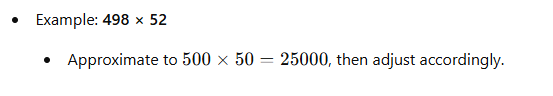
4. Use Vedic Math Techniques
- Cross Multiplication for Fractions:
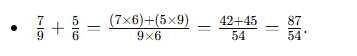
- Multiplication using Vertically and Crosswise Method.
5. Identify Patterns & Shortcuts
- Recognize number sequences, factorial properties, and power rules.

6. Practice Timed Tests
- Solve previous years’ question papers and set a time limit.
- Use mock tests and time yourself to improve speed under pressure.
7. Skip & Return Strategy
- If a question is too long or complex, skip it and come back later. Don’t waste time stuck on one problem.
8. Learn Calculator Tricks (If Allowed)
- If calculators are permitted, learn quick key sequences to solve problems faster.
Would you like specific tricks for a particular math topic? 😊
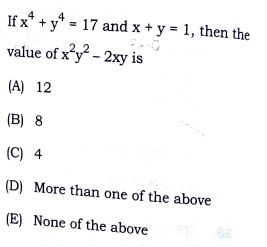
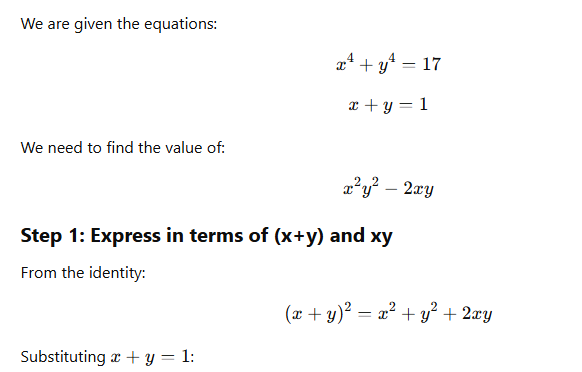


What knowledge i need to solve this math questions
To solve this type of math question efficiently, you need a strong understanding of algebraic identities, quadratic expressions, and equation manipulation. Below are the key concepts required:
1. Algebraic Identities
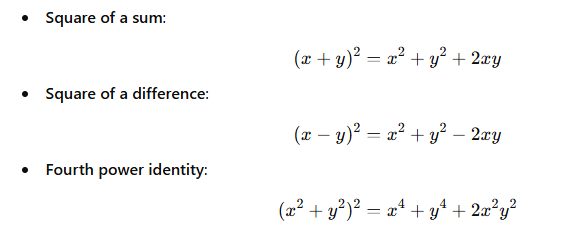
2. Working with Given Equations
- When given x+y and another equation involving higher powers, express terms in terms of xy (product of roots) to simplify calculations.
3. Polynomial Expansion & Factorization
- Recognizing patterns such as
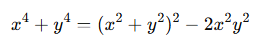
- helps in breaking down the given expressions into solvable forms.
4. Substitution & Equation Solving
- Using known values to substitute in identities and simplify.
5. Problem-Solving Strategy
- Start by rewriting higher-degree terms using known formulas.
- Express everything in terms of simpler variables like xy.
- Use algebraic identities to transform the equation into a solvable form.
Would you like a list of similar problems to practice these concepts? 😊
I know the formula but i not able to think
If you know the formulas but struggle with applying them, the key is pattern recognition and structured thinking. Here’s how you can improve:
1. Break the Problem into Steps
- Don’t try to solve everything at once.
- Identify what you are given and what you need to find.
2. Ask Yourself These Questions
- What formulas are related to the given terms?
- Can I express everything in terms of known quantities?
- Is there a common identity that simplifies the expression?
3. Practice with Similar Problems
- Solve different types of problems that use the same formulas.
- Start with simpler versions of the problem before jumping to complex ones.
4. Work on Speed & Pattern Recognition
- Try recognizing how different expressions fit into known identities.
- The more you practice, the faster your brain will connect the formulas to the problem.
Would you like me to give you a structured approach to solving similar problems step by step? 😊
