Mind Map: Functions, Derivatives & Economic Applications
🔹 फंक्शन और इसके प्रकार (Concept & Types of Functions)
📌 गणितीय समीकरण जो इनपुट और आउटपुट के बीच संबंध दिखाता है।
(Mathematical equation showing the relationship between input & output.)
- अलजेब्रिक (Algebraic) – बहुपद (Polynomial), परिमेय (Rational)
- ट्रिगोनोमेट्रिक (Trigonometric) – साइन, कोसाइन आदि
- घातीय और लघुगणकीय (Exponential & Logarithmic)
🔹 अवकलज और इसके नियम (Concepts of Derivatives & Rules of Differentiation)
📌 किसी फलन में परिवर्तन की दर।
(Rate of change in a function.)
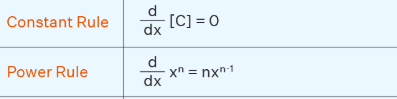
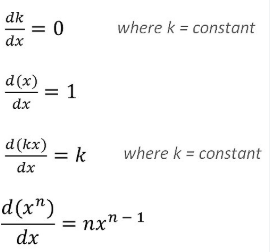
- नियम (Rules):
- योगफल नियम (Sum Rule)
- गुणनफल नियम (Product Rule)
- भागफल नियम (Quotient Rule)
- श्रृंखला नियम (Chain Rule)
🔹 अर्थशास्त्र में अवकलज का उपयोग (Applications of Derivatives in Economics)
📌 विभिन्न आर्थिक गणनाओं में सहायक।
(Helps in various economic calculations.)
- राजस्व (Revenue) – कुल, औसत, सीमांत राजस्व
- लागत (Cost) – कुल, औसत, सीमांत लागत
- मांग और आपूर्ति (Demand & Supply Functions) – लचीलापन और संतुलन बिंदु
- लाभ अधिकतमकरण (Profit Maximization) – MR = MC सिद्धांत
- लचीलापन (Elasticity & Its Types) – कीमत, आय और क्रॉस लचीलापन
📌 निष्कर्ष (Conclusion):
अवकलन अर्थशास्त्र में महत्वपूर्ण उपकरण है जो लागत, लाभ, मांग और आपूर्ति के विश्लेषण में सहायता करता है।
(Differentiation is a key tool in economics, aiding in the analysis of cost, profit, demand, and supply.)
Mind Map: Partial Differentiation & Integration in Economics
🔹 आंशिक अवकलन (Partial Differentiation)
📌 एकाधिक चर वाले फलनों के लिए परिवर्तन की दर का अध्ययन।
(Study of rate of change for functions with multiple variables.)

- नियम (Rules):
- प्रथम और द्वितीय क्रम अवकलज (First & Second Order Partial Derivatives)
- मिश्रित अवकलज (Mixed Derivatives)
- तुल्यता प्रमेय (Clairaut’s Theorem)
🔹 होमोजिनियस फंक्शन और ऑयलर का प्रमेय (Homogeneous Function & Euler’s Theorem)
📌 होमोजिनियस फंक्शन: यदि किसी फलन के सभी चरों को समान गुणांक से गुणा करने पर वह उसी गुणांक की घात से प्रभावित होता है।
(A function where all variables are multiplied by the same factor and result scales accordingly.)
📌 ऑयलर का प्रमेय: होमोजिनियस फलन में चर और उनके आंशिक अवकलजों का संबंध दर्शाता है।
(Relates a homogeneous function to its partial derivatives.)
🔹 उत्पादन फलन (Production Functions)
📌 आर्थिक उत्पादन में श्रम और पूंजी के योगदान का विश्लेषण।
(Analyzing labor & capital contributions in production.)
- Cobb-Douglas Production Function – अर्थशास्त्र में व्यापक रूप से उपयोग।
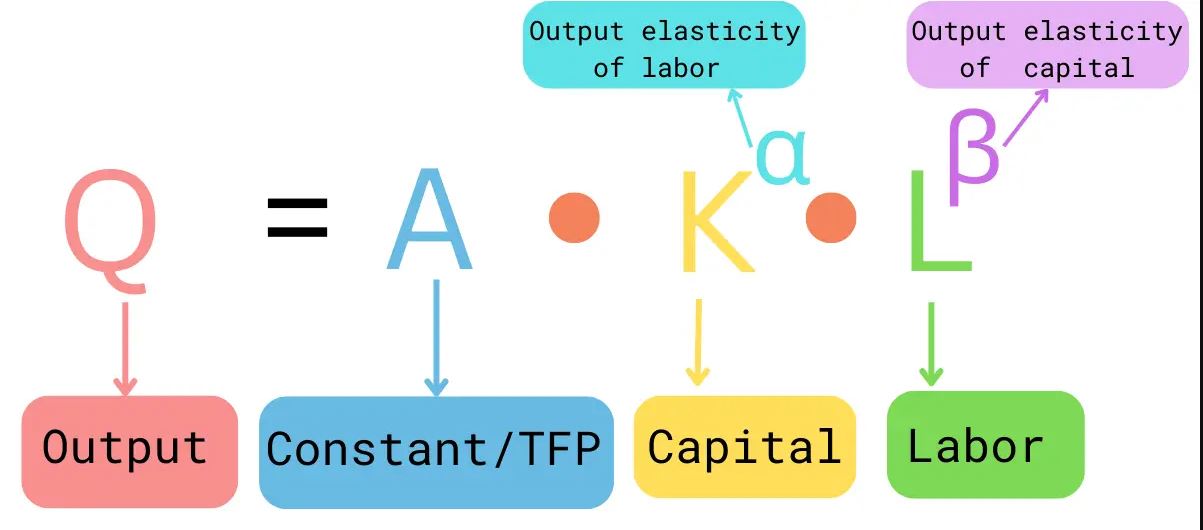
- CES (Constant Elasticity of Substitution) Production Function – पूंजी और श्रम के बीच प्रतिस्थापन की लचीलापन दर।
🔹 समाकलन और अर्थशास्त्र में अनुप्रयोग (Integration & Its Applications in Economics)
📌 किसी फलन के क्षेत्रफल की गणना के लिए उपयोगी।
(Used to calculate the area under a function.)

- निश्चित समाकलन (Definite Integration) – सीमित दायरे में समाकलन।
- अर्थशास्त्र में समाकलन (Integration in Economics) – उपभोक्ता एवं उत्पादक अधिशेष की गणना।
- उपभोक्ता अधिशेष (Consumer Surplus) – भुगतान करने की इच्छा और वास्तविक भुगतान का अंतर।
- उत्पादक अधिशेष (Producer Surplus) – वास्तविक प्राप्ति और न्यूनतम स्वीकार्य कीमत का अंतर।
📌 निष्कर्ष (Conclusion):
आंशिक अवकलन और समाकलन अर्थशास्त्र में मांग, उत्पादन और अधिशेष की गणना में महत्वपूर्ण भूमिका निभाते हैं।
(Partial differentiation & integration play a crucial role in analyzing demand, production, and surplus in economics.)
Mind Map: Matrices, Determinants, and Vectors
🔹गुणनखंड (Determinants) और उनकी विशेषताएँ
📌 गणितीय फलन जो एक वर्ग मैट्रिक्स से एकल स्केलर मान निकालता है।
(A mathematical function that extracts a single scalar value from a square matrix.)
- आधारभूत गुण (Basic Properties) – रेखीयता, आदान-प्रदान गुणधर्म (Swapping rows/columns changes sign), त्रिकोणीय रूपांतरण।
🔹मैट्रिक्स बीजगणित (Matrix Algebra)
📌 संख्याओं के सारणीबद्ध संग्रह जिन पर गणितीय क्रियाएँ की जाती हैं।
(Tabular arrangement of numbers that undergo mathematical operations.)
- प्रकार (Types) – स्केलर, वेक्टर, वर्गीय, विकर्णीय, अभिवर्तन (Transpose), सर्वोत्कृष्ट मैट्रिक्स।
- साधारण क्रियाएँ (Simple Operations) – योग, गुणा, अदला-बदली, स्थानांतरण।
- प्रतिलोम मैट्रिक्स (Matrix Inversion) – किसी मैट्रिक्स का प्रतिलोम तब संभव होता है जब उसका डिटरमिनेंट शून्य न हो।
🔹मैट्रिक्स का कोटि (Rank of Matrix)
📌 मैट्रिक्स में स्वतंत्र पंक्तियों या स्तंभों की अधिकतम संख्या।
(Maximum number of independent rows or columns in a matrix.)
- पूर्ण रैंक (Full Rank)
- शून्य रैंक (Zero Rank)
🔹एकसमान समीकरण हल (Solution of Simultaneous Equations)
📌 कई समीकरणों के समाधान में उपयोगी।
(Useful in solving multiple equations simultaneously.)
- मैट्रिक्स पद्धति (Matrix Method) – गुणा और व्युत्क्रमण द्वारा समाधान।
- क्रैमर का नियम (Cramer’s Rule) – डिटरमिनेंट आधारित विधि।
🔹सदिश (Vector) और उसके गुणधर्म
📌 दिशा और परिमाण वाला गणितीय तत्व।
(A mathematical entity with direction and magnitude.)
- सदिशों का योग और गुणा
- दिशाओं के बीच संबंध
- अनुप्रयोग – भौतिकी और गणित में प्रयोग।
📌 निष्कर्ष (Conclusion):
मैट्रिक्स और डिटरमिनेंट्स गणित और अर्थशास्त्र में समीकरण हल करने, डेटा विश्लेषण, और सांख्यिकी में महत्वपूर्ण भूमिका निभाते हैं।
(Matrices and determinants play a crucial role in solving equations, data analysis, and statistics in mathematics and economics.)
माइंड मैप: बाधित अनुकूलन (Constrained Optimization) और लैग्रेंज गुणक (Lagrangian Multiplier)
🔹 बाधित अनुकूलन (Constrained Optimization)
📌 किसी उद्देश्य फलन (Objective Function) को कुछ शर्तों के अधीन अधिकतम या न्यूनतम करना।
(Maximizing or minimizing an objective function under certain constraints.)
- उदाहरण (Examples): बजट सीमाएं, संसाधन आवंटन, उत्पादन सीमा।
🔹 लैग्रेंज गुणक (Lagrangian Multiplier)
📌 गणितीय तकनीक जो बाधाओं के साथ अनुकूलन की सुविधा देती है।
(A mathematical technique for optimizing functions with constraints.)
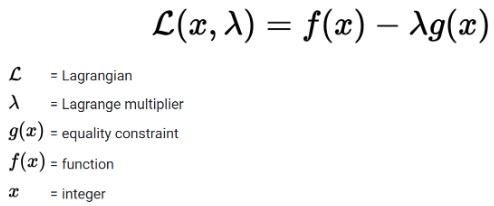
- समीकरण: L=f(x,y)+λ(g(x,y)−c)\mathcal{L} = f(x,y) + \lambda(g(x,y) – c)
- अर्थशास्त्र में उपयोग (Applications in Economics):
- बजट सीमा के तहत उपयोगिता अधिकतमकरण।
- लागत और संसाधन सीमाओं के तहत लाभ अधिकतमकरण।
🔹 उपयोगिता अधिकतमकरण (Maximization of Utility)
📌 उपभोक्ता का उद्देश्य संतुष्टि को अधिकतम करना।
(Consumer’s objective to maximize satisfaction.)
- सीमाएँ (Constraints):
- बजट बाधा
- वस्तुओं की उपलब्धता
- गणितीय दृष्टिकोण (Mathematical Approach):
- लैग्रेंज पद्धति का उपयोग।
- सीमांत उपयोगिता (Marginal Utility) विश्लेषण।
🔹 लाभ अधिकतमकरण (Maximization of Profits)
📌 फर्म का लक्ष्य लागत घटाकर राजस्व बढ़ाना।
(Firm’s objective to maximize revenue while minimizing cost.)
- लाभ फ़ंक्शन (Profit Function): π=TR−TC\pi = TR – TC जहाँ,
- TRTR = कुल राजस्व (Total Revenue)
- TCTC = कुल लागत (Total Cost)
- तकनीक (Techniques):
- लागत-लाभ विश्लेषण
- लैग्रेंज गुणक का उपयोग
📌 निष्कर्ष (Conclusion):
बाधित अनुकूलन और लैग्रेंज गुणक आर्थिक निर्णय लेने के लिए महत्वपूर्ण हैं, विशेष रूप से संसाधन आवंटन, उपयोगिता अधिकतमकरण और लाभ अधिकतमकरण में।
(Constrained optimization and Lagrangian multipliers are crucial for economic decision-making, particularly in resource allocation, utility maximization, and profit maximization.)
माइंड मैप: रैखिक प्रोग्रामिंग (Linear Programming)
🔹 परिचय (Introduction to Linear Programming)
📌 संसाधनों के इष्टतम उपयोग के लिए गणितीय तकनीक।
(A mathematical technique for optimal resource utilization.)
- उदाहरण (Examples): उत्पादन योजना, परिवहन समस्या, बजट आवंटन।
🔹 रैखिक प्रोग्रामिंग समस्या का निर्माण (Formulation of Linear Programming Problem)
📌 किसी समस्या को गणितीय रूप में व्यक्त करना।
(Expressing a problem in mathematical form.)
- उद्देश्य फलन (Objective Function) → अधिकतम या न्यूनतम करना।
- बाधाएँ (Constraints) → सीमाएं, संसाधन, आदि।
- चर (Variables) → निर्णय लेने के लिए आवश्यक तत्व।
🔹 समाधान के प्रकार (Types of Solutions)
- व्यवहार्य हल (Feasible Solution): सभी बाधाओं को संतुष्ट करने वाला हल।
- मूल हल (Basic Solution): स्वतंत्र चर के एक विशिष्ट सेट के साथ व्यवहार्य हल।
- सर्वोत्तम हल (Optimal Solution): उद्देश्य फलन का सर्वोत्तम मान देने वाला हल।
🔹 रेखाचित्र पद्धति द्वारा समाधान (Solution through Graphic Method)
📌 दो चर वाली समस्याओं के लिए दृष्टिगत समाधान।
(Graphical solution method for problems with two variables.)
- व्यवहार्य क्षेत्र (Feasible Region) पहचानना।
- उद्देश्य फलन के स्तर रेखाएँ (Objective Function Lines) खींचना।
- कोने-बिंदु विधि (Corner Point Method) का उपयोग।
🔹 द्वैतता की अवधारणा (Concept of Duality)
📌 प्रत्येक रैखिक प्रोग्रामिंग समस्या का एक द्वैतीय (Dual) रूप होता है।
(Every linear programming problem has a dual form.)
- यदि एक समस्या को हल किया जाता है, तो उसका द्वैतीय स्वतः हल हो जाता है।
- मुख्य रूप से आर्थिक विश्लेषण और संवेदनशीलता विश्लेषण में उपयोग।
📌 निष्कर्ष (Conclusion):
रैखिक प्रोग्रामिंग संसाधन आवंटन और निर्णय लेने की प्रक्रिया को सरल बनाती है, और इसका उपयोग उद्योग, व्यापार, परिवहन और अर्थशास्त्र में व्यापक रूप से किया जाता है।
(Linear programming simplifies resource allocation and decision-making processes and is widely used in industry, business, transportation, and economics.)
माइंड मैप: इनपुट-आउटपुट विश्लेषण और गेम थ्योरी
🔹 इनपुट-आउटपुट विश्लेषण (Input-Output Analysis)
📌 अर्थ और मूल अवधारणाएँ (Meaning and Basic Concepts)
(Analyzing the interdependence of industries in an economy.)
- उत्पादन प्रक्रिया में संसाधनों का प्रवाह।
- उपभोक्ता और उत्पादक के बीच परस्पर संबंध।
📌 खुली और बंद प्रणाली (Open and Closed Models)
- खुली प्रणाली (Open Model): बाहरी कारकों से प्रभावित होती है।
- बंद प्रणाली (Closed Model): आत्मनिर्भर प्रणाली, बाहरी प्रभाव नहीं।
📌 स्थिर और गतिशील मॉडल (Static and Dynamic Models)
- स्थिर मॉडल (Static Model): समय के साथ परिवर्तन को नहीं दर्शाता।
- गतिशील मॉडल (Dynamic Model): समय के साथ परिवर्तन और विकास को दर्शाता है।
🔹 गेम थ्योरी (Game Theory)
📌 बुनियादी अवधारणाएँ (Basic Concepts of Game Theory)
(Mathematical study of strategy in decision-making.)
- विभिन्न खिलाड़ियों के बीच रणनीतिक बातचीत।
- एक खिलाड़ी का लाभ दूसरे की रणनीति पर निर्भर करता है।
📌 शून्य योग और गैर-शून्य योग खेल (Zero-Sum and Non-Zero Sum Games)
- शून्य योग खेल (Zero-Sum Game): एक खिलाड़ी का लाभ, दूसरे का नुकसान। (Example: शतरंज, पोकर)
- गैर-शून्य योग खेल (Non-Zero Sum Game): सभी खिलाड़ी लाभ उठा सकते हैं। (Example: व्यापार वार्ता, सहयोगी खेल)
📌 शुद्ध और मिश्रित रणनीति (Pure and Mixed Strategy)
- शुद्ध रणनीति (Pure Strategy): पूर्व निर्धारित चालों के आधार पर निर्णय।
- मिश्रित रणनीति (Mixed Strategy): संभाव्यता के आधार पर निर्णय।
📌 निष्कर्ष (Conclusion)
इनपुट-आउटपुट विश्लेषण से आर्थिक संसाधनों के प्रवाह को समझा जाता है, जबकि गेम थ्योरी रणनीतिक निर्णय लेने में सहायक होती है। दोनों का उपयोग अर्थशास्त्र, व्यापार, और सामाजिक विज्ञान में किया जाता है।
