Unit 11: Theory of Computation

Introduction; Alphabets, Strings and Languages; Automata and Grammars, Deterministic finite Automata (DFA)-Formal Definition, Simplified notation: State transition graph, Transition table, Language of DFA, Non-deterministic finite Automata (NFA), NFA with epsilon transition, Language of NFA, Equivalence of NFA and DFA, Minimization of Finite Automata, Distinguishing one string from other.

📘 1. Introduction (परिचय)

Automata Theory वह शाखा है जो यह समझाती है कि कंप्यूटर या मशीनें कैसे भाषा को पहचानती और प्रोसेस करती हैं।

यह मुख्य रूप से तीन चीजों पर आधारित है:

Alphabets
Strings
Languages

🔤 2. Alphabets, Strings, and Languages

👉 Alphabets (वर्णमाला)

एक finite set of symbols
उदाहरण: {0, 1} या {a, b, c}

👉 Strings (स्ट्रिंग्स)

Alphabets का एक क्रम (sequence)
जैसे: "101", "ab", "aabb"

👉 Language (भाषा)

स्ट्रिंग्स का सेट जो किसी नियम या ऑटोमेटा द्वारा स्वीकारे जाते हैं।
उदाहरण: सभी स्ट्रिंग्स जो "a" से शुरू होती हैं।

🤖 3. Automata and Grammars

Automata (स्वचालित मशीनें): एक mathematical model जो input को process करके बताता है कि वह स्वीकार्य है या नहीं।
Grammar (व्याकरण): यह यह परिभाषित करती है कि कोई भाषा कैसे बनती है। (जैसे Regular Grammar, Context-Free Grammar)

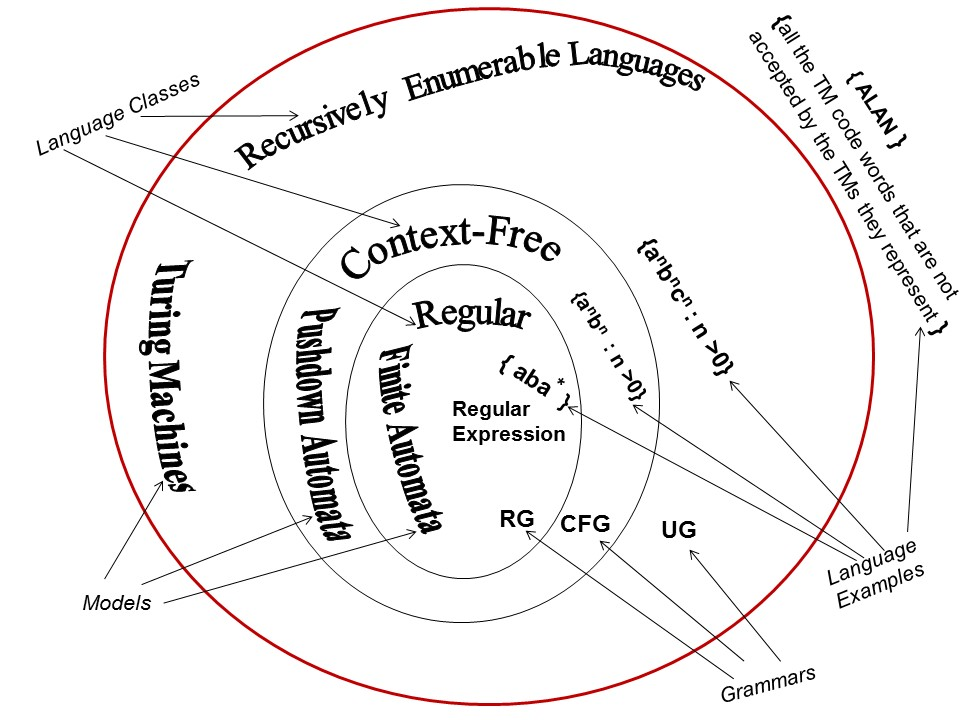
⚙️ 4. Deterministic Finite Automata (DFA)

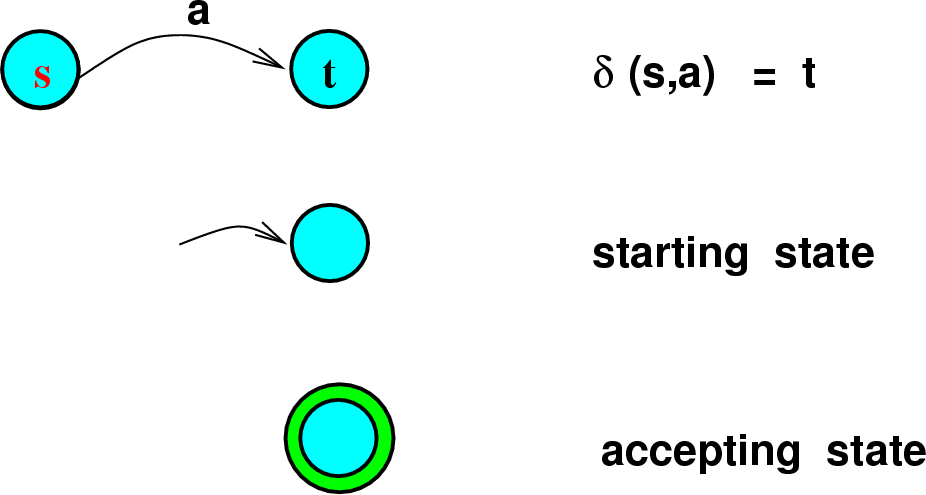
👉 परिभाषा:

DFA एक finite automata है जिसमें हर स्थिति (state) पर, हर input symbol के लिए सिर्फ एक next state होती है।

📌 Formal Definition:

DFA को 5-टुपल में परिभाषित किया जाता है:

M=(Q, Σ, δ, q0, F)

जहाँ:

Q: सभी states का finite set
Σ: input alphabets
δ: transition function (Q × Σ → Q)
q: initial state
F: final/accepting states का सेट

📊 5. Simplified Notation

🔹 State Transition Graph:

Nodes = States
Arrows = Input transitions
एक ग्राफ जो बताता है input के अनुसार control कैसे flow होता है।

🔹 Transition Table:

State	Input 0	Input 1
q0	q1	q2
q1	q0	q2

🌐 6. Language of DFA

DFA जिन-जिन स्ट्रिंग्स को स्वीकार करता है, उनका सेट उस DFA की language कहलाता है।

🔁 7. Non-Deterministic Finite Automata (NFA)

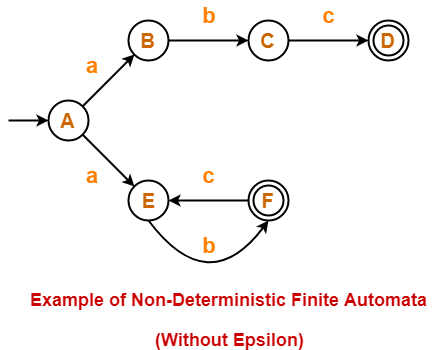
👉 परिभाषा:

NFA में किसी भी input symbol के लिए multiple transitions हो सकती हैं या कोई नहीं भी।
यानी एक ही स्थिति पर एक से ज्यादा रास्ते हो सकते हैं।

🤍 NFA with ε (epsilon) transitions:

कुछ transitions बिना किसी input के होते हैं (ε-move)।
यह मशीन बिना input consume किए एक state से दूसरी में जा सकती है।

🔄 8. Language of NFA

NFA की भी एक भाषा होती है — वह सेट जिसमें आने वाली स्ट्रिंग्स को वह स्वीकार करता है।

🔁 9. Equivalence of NFA and DFA

सिद्ध किया जा चुका है कि हर NFA का एक equivalent DFA होता है।
इसका मतलब है: NFA और DFA की computational power समान होती है।
Subset construction algorithm का उपयोग करके NFA से DFA बनाया जाता है।

🔽 10. Minimization of Finite Automata

DFA को छोटा और सरल बनाने की प्रक्रिया, ताकि उसमें कम से कम states हों।
इससे memory और प्रोसेसिंग दोनों में लाभ होता है।
Equivalent states को merge करके यह किया जाता है।

🆚 11. Distinguishing One String from Other

यह समझने की प्रक्रिया कि कोई दो स्ट्रिंग्स किसी language के लिए अलग-अलग व्यवहार क्यों करती हैं।
उदाहरण: एक string को DFA स्वीकार कर रहा है, दूसरी को नहीं — क्यों?

✅ संक्षेप सारांश (Summary Table)

टॉपिक	विवरण
Alphabets	Symbols का finite set
Strings	Alphabets का क्रम
Language	स्ट्रिंग्स का सेट जो किसी ऑटोमेटा को स्वीकार हो
DFA	एक निश्चित finite मशीन
NFA	एक अनिश्चित मशीन जिसमें multiple transitions हो सकती हैं
ε-NFA	NFA जिसमें बिना input के transitions हो सकती हैं
DFA vs NFA	दोनों समान शक्ति वाले हैं
Minimization of DFA	States को merge कर छोटा बनाना
Distinguishing Strings	स्ट्रिंग्स को अलग पहचान देना

Regular expression (RE) , Definition, Operators of regular expression and their precedence, Algebraic laws for Regular expressions, Kleen’s Theorem, Regular expression to FA, DFA to Regular expression, Arden Theorem, Non Regular Languages, Pumping Lemma for regular Languages . Application of Pumping
Lemma, Closure properties of Regular Languages, Decision properties of Regular Languages, FA with output: Moore and Mealy machine, Equivalence of Moore and Mealy Machine, Applications and Limitation of FA.

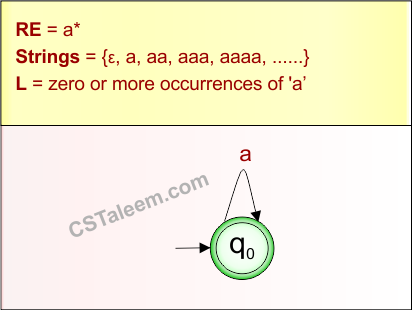
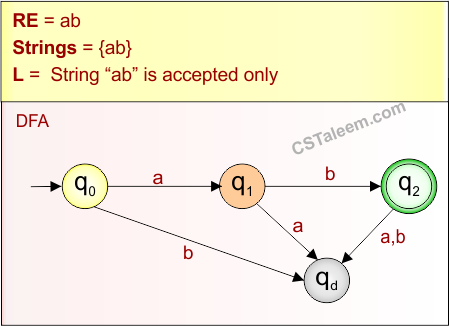
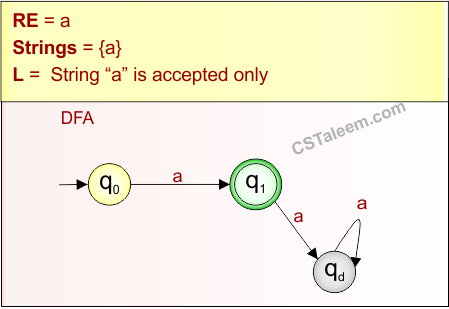
🔁 1. Regular Expression (RE) – रेगुलर एक्सप्रेशन

👉 परिभाषा (Definition):

Regular Expression (RE) एक तरीका है जिससे हम किसी Regular Language को symbolic रूप में व्यक्त करते हैं।
यह describe करता है कि किस तरह की string उस language में आ सकती है।

➕ 2. Operators of Regular Expression and Their Precedence

🔹 मुख्य ऑपरेटर:

ऑपरेटर	कार्य
`+` (Union)	दो languages का जोड़ (OR)
`.` (Concatenation)	दो strings को जोड़ना
`*` (Kleene Star)	0 या अधिक बार दोहराना

🔸 Precedence (Priority):

* (सबसे पहले लागू होता है)
. (Concatenation)
+ (Union)

🧮 3. Algebraic Laws for Regular Expressions

कुछ महत्वपूर्ण नियम:

Identity:
- R + ∅ = R
- R.ε = R
Annihilation:
- R.∅ = ∅
Distributive Laws:
- R.(S + T) = R.S + R.T
- (R + S).T = R.T + S.T

💡 4. Kleene’s Theorem

Kleene’s Theorem बताता है कि:

हर Regular Expression के लिए एक Finite Automaton (FA) होता है।
और हर FA के लिए एक Regular Expression होता है।

👉 इससे RE और FA के बीच equivalence साबित होती है।

🔄 5. Regular Expression to Finite Automata (RE → FA)

किसी भी regular expression से हम एक NFA (non-deterministic finite automaton) बना सकते हैं जो उसे recognize करता है।

🔁 6. DFA to Regular Expression (DFA → RE)

किसी भी DFA को हम step by step modify करके एक regular expression में बदल सकते हैं।

🔢 7. Arden’s Theorem

Arden’s Theorem का उपयोग Regular Expression निकालने के लिए किया जाता है जब हमें equations के रूप में state transitions दिए गए हों।

👉 Useful in DFA → RE conversion.

Statement:
अगर equation है:

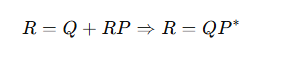
🚫 8. Non-Regular Languages

कुछ languages को हम किसी finite automaton या regular expression से describe नहीं कर सकते।
जैसे: {a^n b^n | n ≥ 0}
ये languages non-regular होती हैं।

💣 9. Pumping Lemma for Regular Languages

👉 क्या है?

एक तरीका जिससे हम यह साबित कर सकते हैं कि कोई language regular नहीं है।

📌 Statement (संक्षेप में):

कोई भी regular language L के लिए कोई constant p (pumping length) होता है, ऐसा कि
हर string s ∈ L जहाँ |s| ≥ p, को 3 हिस्सों में बाँटा जा सकता है: s=xyzs = xyzs=xyz

ऐसे कि:

|y| > 0
|xy| ≤ p
x y^i z ∈ L for all i ≥ 0

🧪 10. Application of Pumping Lemma

Pumping Lemma का उपयोग यह साबित करने में किया जाता है कि कोई language regular नहीं है।
जैसे: {a^n b^n | n ≥ 0} — इसे कोई finite automaton recognize नहीं कर सकता।

🧱 11. Closure Properties of Regular Languages

Regular languages इन operations के तहत closed होती हैं:

Operation	Closed?
Union (`L1 ∪ L2`)	✅ Yes
Intersection	✅ Yes
Complement	✅ Yes
Concatenation	✅ Yes
Kleene Star (`L*`)	✅ Yes

🔍 12. Decision Properties of Regular Languages

हम regular languages पर कुछ सवालों का जवाब algorithmically दे सकते हैं (i.e., decidable):

प्रश्न	उत्तर
क्या string L में है?	✅ हाँ
क्या L empty है?	✅ हाँ
क्या L infinite है?	✅ हाँ
क्या दो DFA एक ही language accept करते हैं?	✅ हाँ

⚙️ 13. FA with Output – Moore and Mealy Machines

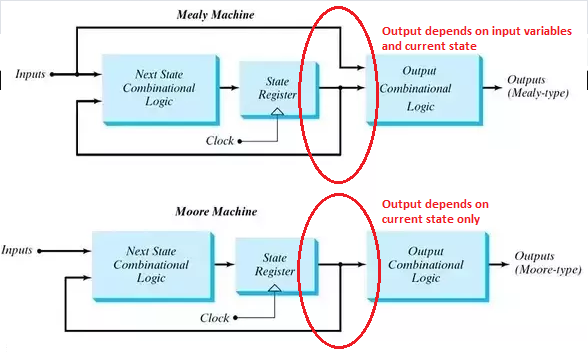
🔸 Moore Machine:

Output केवल state पर निर्भर करता है।
हर state के साथ एक output जुड़ा होता है।

🔸 Mealy Machine:

Output input और current state दोनों पर निर्भर करता है।
Output transitions में होता है।

🔁 14. Equivalence of Moore and Mealy Machine

दोनों machines equivalent होती हैं।
किसी भी Mealy Machine को Moore Machine में और vice-versa बदला जा सकता है।

✅ 15. Applications and Limitations of FA

✔️ Applications:

Compiler design (Lexical analyzer)
Pattern matching
Network protocols
Text processing tools (Regex)

❌ Limitations:

Finite memory होने के कारण complex languages (जैसे palindromes, balanced parentheses) को handle नहीं कर सकता।
Context-sensitive या context-free languages को FA accept नहीं कर सकते।

📚 संक्षेप सारांश (Quick Table):

टॉपिक	विवरण
Regular Expression	Language describe करने का तरीका
DFA, NFA	Languages को accept करने वाली मशीनें
Kleene’s Theorem	RE ⇌ FA के बीच equivalence
Arden’s Theorem	Equation से RE निकालने के लिए
Pumping Lemma	Language regular नहीं है, यह सिद्ध करना
Moore Machine	Output → States पर निर्भर
Mealy Machine	Output → Input + State पर निर्भर
Closure/Decision Properties	Regular languages के गणितीय गुण
Applications	Compiler, Pattern Matching आदि
Limitations	Complex structures accept नहीं कर सकता

Context free grammar (CFG) and Context Free Languages (CFL): Definition, Examples, Derivation ,Derivation trees, Ambiguity in Grammer, Inherent ambiguity, Ambiguous to Unambiguous CFG, Useless symbols, Simplification of CFGs, Normal forms for CFGs: CNF and GNF, Closure properties of CFLs, Decision Properties of CFLs: Emptiness, Finiteness and Memership, Pumping lemma for CFLs.

📘 1. Context Free Grammar (CFG) – परिभाषा और उदाहरण

👉 परिभाषा:

Context-Free Grammar एक grammar होती है जिसका हर production rule निम्न प्रकार का होता है:

A→αA

जहाँ:

A = एक non-terminal symbol
α = एक string जो terminals और/or non-terminals का समूह हो सकती है

👉 यह grammar उन भाषाओं को define करती है जो context-free होती हैं।

📌 Example of CFG:

S → aSb | ε

यह grammar {a^n b^n | n ≥ 0} language को generate करती है।

🌐 2. Context Free Languages (CFL)

CFLs वे भाषाएँ हैं जिन्हें कोई Context-Free Grammar generate कर सकती है।

उदाहरण:

Palindromes
Balanced parentheses
a^n b^n

🔄 3. Derivation and Derivation Trees

📌 Derivation:

Grammar के rules को step-by-step apply कर के किसी string को generate करना।

उदाहरण:

S → aSb → aaSbb → ε → aabb

🌳 Derivation Tree / Parse Tree:

एक tree structure जो derivation को graphically दिखाता है।
Root = Start symbol
Leaves = Final string के characters

🤔 4. Ambiguity in Grammar (ग्रामर में अस्पष्टता)

अगर किसी string की एक से अधिक derivation trees या parse trees बनती हैं, तो वह grammar ambiguous कहलाती है।

उदाहरण: Arithmetic expressions में ambiguity हो सकती है।

⚠️ 5. Inherent Ambiguity

कुछ languages ऐसी होती हैं जिनके लिए कोई भी CFG unambiguous नहीं हो सकती।
उन्हें कहते हैं — Inherently ambiguous languages

🔁 6. Ambiguous to Unambiguous CFG

कई बार हम ambiguous grammar को modify कर के उसे unambiguous बना सकते हैं।

उदाहरण:
Ambiguous:

E → E + E | E * E | id

Unambiguous:

E → E + T | T
T → T * F | F
F → id

🚫 7. Useless Symbols (बेकार चिन्ह)

Grammar में ऐसे symbols जो:

कभी किसी derivation में use नहीं होते
या किसी string तक नहीं पहुंचते

उन्हें useless symbols कहते हैं और उन्हें grammar से हटाना चाहिए।

🔧 8. Simplification of CFGs

CFG को simplify करने के लिए:

Useless symbols हटाना
Unit productions (A → B) को हटाना
Nullable productions (A → ε) को simplify करना

🧱 9. Normal Forms for CFGs

📌 CNF – Chomsky Normal Form

हर production इस form में होती है:
- A→BC
- A→a
जहाँ A,B,CA, B, CA,B,C non-terminals और aaa terminal है

📌 GNF – Greibach Normal Form

हर production इस रूप में होता है:
- A→aα
यानी हर rule एक terminal से शुरू होता है

👉 CNF और GNF से parsing और proof आसान हो जाता है।

🔒 10. Closure Properties of CFLs

ऑपरेशन	CFLs के लिए Closed?
Union	✅ Yes
Concatenation	✅ Yes
Kleene Star	✅ Yes
Intersection	❌ No
Complement	❌ No

❓ 11. Decision Properties of CFLs

प्रॉपर्टी	CFLs के लिए निर्णय किया जा सकता है?
Emptiness (L = ∅?)	✅ Yes
Finiteness (L finite?)	✅ Yes
Membership (w ∈ L?)	✅ Yes

💣 12. Pumping Lemma for CFLs

👉 उपयोग:

यह साबित करने के लिए कि कोई भाषा context-free नहीं है।

📌 Statement (संक्षेप में):

हर CFL के लिए एक constant p (pumping length) होता है
जिसके लिए कोई भी string s ∈ L, जहाँ |s| ≥ p, को 5 भागों में बाँटा जा सकता है: s=uvwxys = uvwxys=uvwxy

ऐसे कि:

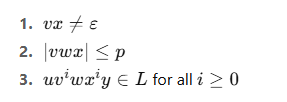
❌ इससे हम यह सिद्ध कर सकते हैं कि कुछ languages CFL नहीं हैं।

📚 संक्षेप सारांश (Summary Table):

टॉपिक	विवरण
CFG	Grammar जो context-free languages generate करे
CFL	Languages जो किसी CFG से बनती हैं
Derivation	Grammar rules से string बनाना
Parse Tree	Derivation को tree रूप में दिखाना
Ambiguity	जब एक से ज्यादा parse trees बनें
Inherent Ambiguity	Language में ambiguity को हटाया नहीं जा सकता
Useless Symbols	ऐसे symbols जो derivation में काम न आएं
CNF, GNF	Grammar के simplified standard forms
Closure Properties	Union, Concatenation, Star = Closed
Decision Properties	Emptiness, Finiteness, Membership = Decidable
Pumping Lemma for CFL	Prove करने के लिए कि language CFL नहीं है

Push Down Automata (PDA): Description and definition, Instantaneous Description, Language of PDA, Acceptance by Final state, Acceptance by empty stack, Deterministic PDA, Equivalence of PDA and CFG, CFG to PDA and PDA to CFG, Two stack PDA

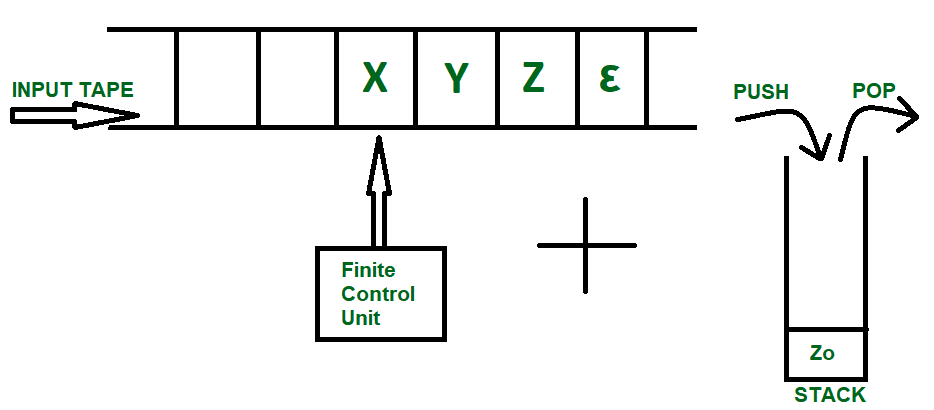
🧠 1. PDA – परिचय और परिभाषा

📌 Push Down Automata (PDA) क्या होता है?

PDA एक Finite Automaton (FA) की तरह ही होता है,
लेकिन इसमें एक Stack भी होता है जो इसे ज़्यादा पावरफुल बनाता है।

PDA का उपयोग Context Free Languages (CFLs) को recognize करने के लिए किया जाता है।

🔹 Formal Definition of PDA:

PDA को एक 7-टुपल के रूप में परिभाषित किया जाता है:

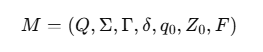
⚡ 2. Instantaneous Description (ID) – क्षणिक विवरण

ID PDA की एक current snapshot होती है, जिसमें होता है: (q,w,γ)(q, w, \gamma)(q,w,γ)

जहाँ:

q = current state
w = input string का बाकी हिस्सा
γ = stack की current स्थिति (top at left)

🌐 3. Language of PDA

PDA उन strings को accept करता है जो किसी context-free language में आती हैं।

🟢 Acceptance के दो तरीके:

✅ 4. Acceptance by Final State

जब PDA input string को पढ़ने के बाद final state में पहुँच जाए — तो वह string accepted मानी जाती है।

🗑️ 5. Acceptance by Empty Stack

जब PDA पूरा input पढ़ ले और उसका stack empty हो जाए, तो वह string accepted मानी जाती है।

📌 दोनों acceptance methods equivalent हैं यानी दोनों से एक ही CFL को recognize किया जा सकता है।

🔄 6. Deterministic PDA (DPDA)

DPDA में हर स्थिति पर एक input और stack symbol के लिए एक ही transition संभव होती है।
सभी CFLs को DPDA से recognize नहीं किया जा सकता।

प्रकार	ताक़त
Non-Deterministic PDA	सभी CFLs
Deterministic PDA	कुछ CFLs ही

🔁 7. Equivalence of PDA and CFG

PDA और CFG एक-दूसरे के लिए equivalent हैं।

हर CFG के लिए एक PDA exist करता है जो उसी language को accept करता है।
और हर PDA के लिए एक CFG बनाई जा सकती है।

📤 8. CFG to PDA

✅ विचार:

जब भी grammar का कोई rule हो A → α,
तो PDA stack पर A को हटाकर α को push कर देगा।

👉 यह PDA stack का उपयोग derivation को simulate करने के लिए करता है।

📥 9. PDA to CFG

PDA के transitions से हम एक grammar construct कर सकते हैं जो उसी language को generate करेगी।

👉 इसमें हर PDA की state के pair के लिए एक non-terminal define किया जाता है।

🧱 10. Two-Stack PDA

💡 एक PDA जिसमें दो stacks हों, वह एक Turing Machine के equivalent हो जाता है।

🧠 ताकत:

दो stacks की मदद से PDA context-sensitive और recursively enumerable languages को भी accept कर सकता है।

Automaton	ताक़त (Power)
FA	Regular Languages
PDA (1 stack)	Context Free Languages
2-stack PDA / TM	Turing complete (all languages)

📝 संक्षेप सारांश (Summary Table)

टॉपिक	विवरण
PDA	Stack वाला FA — CFLs के लिए उपयोगी
ID (Instantaneous Description)	PDA की current स्थिति की जानकारी
Acceptance (Final/Empty)	PDA string को final state या empty stack से स्वीकार कर सकता है
DPDA vs NPDA	DPDA कुछ CFLs ही accept करता है
PDA ⇄ CFG	दोनों एक-दूसरे के बराबर (equivalent) हैं
Two-stack PDA	Turing machine के बराबर शक्तिशाली

Context Sensitive Languages (CSL) और Linear Bounded Automata (LBA)

📘 1. Context Sensitive Languages (CSL)

👉 परिभाषा:

Context Sensitive Languages वे भाषाएँ होती हैं जिन्हें Context Sensitive Grammar (CSG) से generate किया जा सकता है।

📌 Grammar Rules:

Context Sensitive Grammar में हर production rule इस रूप में होता है:

αAβ→αγβ

जहाँ:

A एक non-terminal है,
α,β किसी भी string हो सकते हैं (terminals या non-terminals),
γ एक non-empty string होनी चाहिए।

और सबसे महत्वपूर्ण बात:

∣αAβ∣≤∣αγβ∣

🔹 यानी कोई भी production rule string की लंबाई को घटा नहीं सकता
(Null production की अनुमति नहीं होती, सिवाय एक exception के लिए: S→εS \rightarrow \varepsilonS→ε, अगर ε language में है और S कहीं और use नहीं होता)

🎯 उदाहरण:

Language: L={anbncn∣n≥1}L = \{ a^n b^n c^n \mid n \geq 1 \}L={anbncn∣n≥1}

यह language context-free नहीं है, लेकिन यह context-sensitive है।

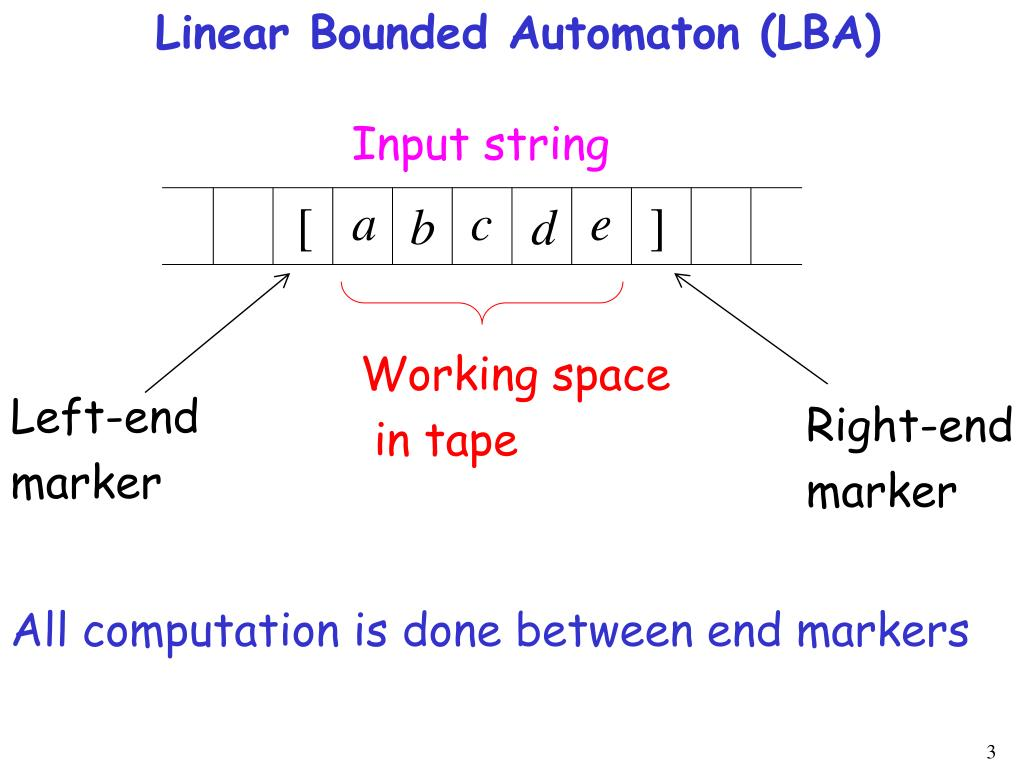
🧠 2. Linear Bounded Automata (LBA)

👉 परिभाषा:

Linear Bounded Automaton (LBA) एक विशेष प्रकार की Turing Machine है जिसकी tape size सीमित होती है — यानी input के आकार के अनुसार ही tape मिलता है।

🧱 Structure:

Turing Machine की तरह ही होता है।
लेकिन tape की length ≤ length of input × constant।

📌 Key Features:

विशेषता	विवरण
टेप	केवल input की length तक सीमित होता है
हेड	Left-most और right-most सीमाएं पार नहीं कर सकता
शक्तियाँ	Context-sensitive languages को accept करता है

🔁 3. संबंध: CSL ⇄ LBA

Model/Grammar	Language Class
Context Sensitive Grammar (CSG)	Context Sensitive Languages (CSL)
Linear Bounded Automaton (LBA)	Context Sensitive Languages (CSL)

👉 मतलब:
LBA और CSG दोनों एक ही class की languages को recognize/generate करते हैं — Context Sensitive Languages।

🧾 4. Language Hierarchy (Chomsky Hierarchy)

यहाँ पर पूरी hierarchy दिखाई गई है जो computational power को दर्शाती है:

Type-0 (Recursively Enumerable) — Turing Machine  
   ⬇  
Type-1 (Context Sensitive) — LBA  
   ⬇  
Type-2 (Context Free) — PDA  
   ⬇  
Type-3 (Regular) — FA

👉 हर ऊपर वाला class नीचे वाले से ज़्यादा शक्तिशाली होता है।

🔐 5. Important Points & Differences

विषय	Context-Free (PDA)	Context-Sensitive (LBA)
Grammar Type	Type-2	Type-1
Automaton Type	PDA	LBA (Restricted TM)
Accepted Language	aⁿbⁿ	aⁿbⁿcⁿ
Memory	Stack	Bounded Tape
Null Production Allowed?	हाँ	नहीं (length can’t decrease)

❓ क्या Context Sensitive Languages Decidable होती हैं?

👉 हाँ, CSLs are decidable — यानी उनके लिए एक TM exist करता है जो हमेशा halt करेगी।

📘 संक्षेप सारांश (Quick Recap):

टॉपिक	विवरण
CSL	Context Sensitive Language (Type-1)
CSG	Context Sensitive Grammar
LBA	Restricted Turing Machine
Power	PDA से ज्यादा, TM से कम
Example Language	`{aⁿbⁿcⁿ}`

Turing machines (TM): Basic model, definition and representation,
Instantaneous Description, Language acceptance by TM, Variants of Turing Machine, TM as Computer of Integer functions, Universal TM, Church’s Thesis, Recursive and recursively enumerable languages, Halting problem, Introduction to Undecidability, Undecidable problems about TMs. Post
correspondence problem (PCP), Modified PCP, Introduction to recursive function theory

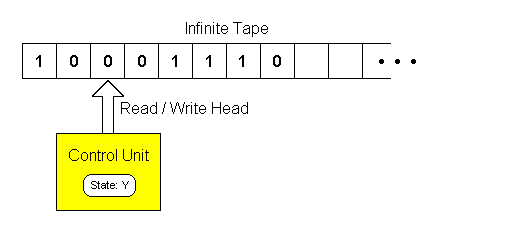
📘 1. Turing Machine (TM) – मूल मॉडल और परिभाषा

📌 परिभाषा:

Turing Machine (TM) एक theoretical model है जो एक infinite tape, एक head और एक finite control (state machine) के साथ काम करता है।

यह मशीन किसी भी computable function को हल कर सकती है — यानी, यह एक idealized computer की तरह है।

🧱 2. Components of Turing Machine

Component	कार्य
Infinite Tape	Input/output और intermediate data रखने के लिए
Tape Head	एक cell पढ़ता और लिखता है, left/right move करता है
State Control	Current state के आधार पर transition करता है

🔹 Formal Definition:

TM को 7-टुपल में परिभाषित किया जाता है:

🧾 3. Instantaneous Description (ID)

ID = Turing Machine की वर्तमान स्थिति का snapshot:

αqβ

जहाँ:

α = tape का left हिस्सा
q = current state
β = head के नीचे और उसके बाद के tape contents

🌐 4. Language Acceptance by TM

Turing Machine एक language को accept करती है अगर:

वह input को पढ़ने के बाद final (accepting) state में पहुँच जाए।
इसे कहते हैं — TM accepts the string.

🔁 5. Variants of Turing Machine

प्रकार	विवरण
Multi-tape TM	एक से अधिक tapes होती हैं
Non-deterministic TM	हर input पर कई transitions possible
Multi-head TM	एक ही tape पर multiple heads
TM with Stay Option	Head को रुकने की अनुमति

👉 ये सभी equivalent in power होते हैं (i.e. एक-दूसरे को simulate कर सकते हैं)।

🧮 6. TM as Computer of Integer Functions

Turing Machine का उपयोग केवल language accept करने के लिए नहीं,
बल्कि किसी भी integer function को compute करने के लिए भी किया जा सकता है,
जैसे:

Addition
Multiplication
Factorial

🌍 7. Universal Turing Machine (UTM)

यह एक ऐसा Turing Machine है जो किसी भी दूसरे TM को simulate कर सकती है।

👉 यह एक general-purpose computer की तरह होती है।
👉 UTM को input के साथ किसी दूसरे TM का description दिया जाता है।

🧠 8. Church’s Thesis

Church और Turing का कहना था कि:

“जो भी problem algorithm से हल की जा सकती है, उसे Turing Machine से हल किया जा सकता है।”

👉 यह theoretical आधार है computability का।

🔁 9. Recursive और Recursively Enumerable Languages

प्रकार	विवरण
Recursive Languages (R)	हर input के लिए TM halt करती है और सही निर्णय देती है (accept/reject)
Recursively Enumerable (RE)	अगर string language में है तो TM accept करेगी, लेकिन reject के लिए halt जरूरी नहीं

👉 हर recursive language, RE भी होती है, पर हर RE language recursive नहीं होती।

⛔ 10. Halting Problem

🧩 परिभाषा:

यह जानना कि कोई Turing Machine किसी input पर halt करेगी या नहीं, यह undecidable है।

👉 इसका कोई general algorithm नहीं हो सकता।

🚫 11. Introduction to Undecidability

कुछ problems ऐसे होते हैं जिन्हें किसी भी algorithm से हल नहीं किया जा सकता, यानी:

❌ कोई Turing Machine exist नहीं करती जो सभी cases में सही निर्णय दे सके।

उन्हें कहते हैं — Undecidable Problems

🔐 12. Undecidable Problems about TMs

Problem	Status
TM halts on input www?	❌ Undecidable
Two TMs accept same language?	❌ Undecidable
TM accepts all strings?	❌ Undecidable
TM accepts empty language?	❌ Undecidable

💌 13. Post Correspondence Problem (PCP)

🔸 परिभाषा:

PCP में आपको दो lists of strings दी जाती हैं:

A = [a₁, a₂, …, aₙ]
B = [b₁, b₂, …, bₙ]

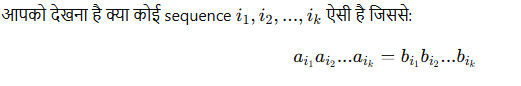
👉 PCP एक classic undecidable problem है।

🛠️ 14. Modified PCP (MPCP)

🔢 15. Introduction to Recursive Function Theory

यह theory यह अध्ययन करती है कि कौन-कौन से functions effectively computable हैं।

यह तीन मुख्य functions से शुरू होती है:

Zero Function
Successor Function
Projection Function

और उनके combination से complex recursive functions बनते हैं।

📘 संक्षेप सारांश (Quick Recap)

टॉपिक	विवरण
TM	कंप्यूटेशन का सबसे पावरफुल मॉडल
UTM	General-purpose TM
Recursive vs RE	R ⊆ RE
Halting Problem	Undecidable
Undecidable TM Problems	कई महत्वपूर्ण सवालों का हल नहीं
PCP / MPCP	Matching problem → Undecidable
Recursive Function Theory	Computable functions का अध्ययन