Unit 3: Programming and data structure

Introduction

🔹 Programming क्या होता है?

Programming एक प्रक्रिया है जिसमें हम कंप्यूटर को निर्देश (instructions) देते हैं ताकि वह कोई विशेष काम कर सके। ये निर्देश हम किसी programming language जैसे C, C++, Python, Java में लिखते हैं।

🧠 Basic Concepts:

Variable – एक container होता है जिसमें हम data store करते हैं।
🧾 उदाहरण: int age = 20;
Data Types – यह data के प्रकार को दर्शाता है:
- int → पूर्णांक
- float → दशमलव संख्या
- char → एक character
- string → टेक्स्ट
- bool → true/false मान
Operators – ये गणितीय और तर्कसंगत operations के लिए होते हैं:
- +, -, *, /, % (Arithmetic Operators)
- ==, !=, <, > (Comparison Operators)
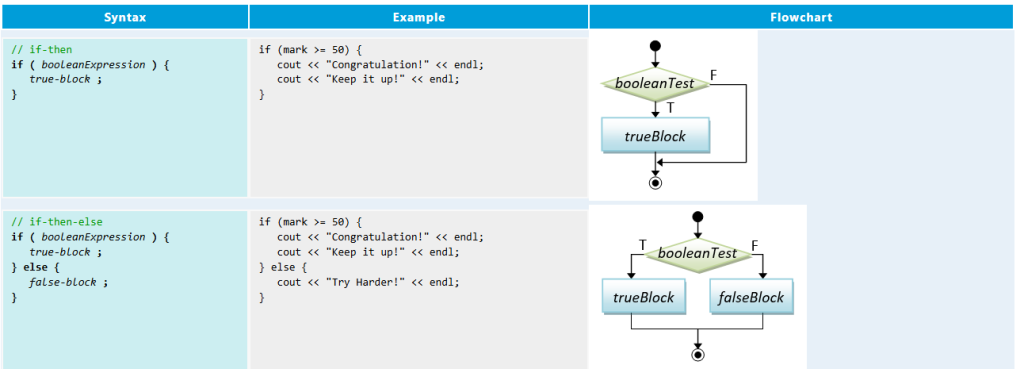
Conditionals – जब हमें किसी condition के आधार पर निर्णय लेना हो: if (age >= 18) { cout << "आप वोट कर सकते हैं"; } else { cout << "आप वोट नहीं कर सकते"; }

5. Loops – जब कोई कार्य बार-बार दोहराना हो:

for, while, do-while

🔹 Data Structures क्या होते हैं?

Data Structures वो तरीके हैं जिनसे हम data को memory में संगठित (organize) करते हैं ताकि उसपर fast और efficient operations किए जा सकें।

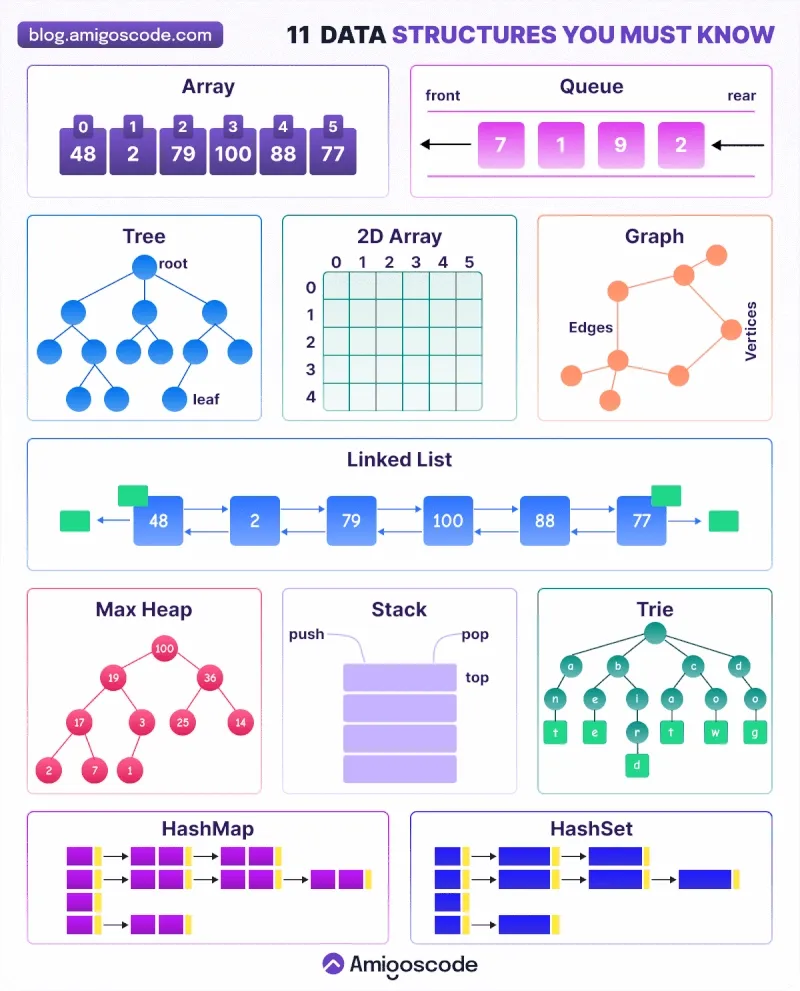
📚 मुख्य Data Structures:

Array
- एक निश्चित आकार का एकसमान प्रकार के data का संग्रह
- उदाहरण: int arr[5] = {1, 2, 3, 4, 5};
Linked List
- data blocks (nodes) जो एक-दूसरे से pointers द्वारा जुड़े होते हैं
- लचीला आकार लेकिन थोड़ा जटिल
Stack (LIFO – Last In First Out)
- जो अंतिम में आता है, वही पहले बाहर जाता है
- उदाहरण: undo ऑप्शन
Queue (FIFO – First In First Out)
- जो पहले आता है, वही पहले जाता है
- उदाहरण: टिकट की लाइन
Tree
- एक hierarchical संरचना (structure)
- उदाहरण: family tree या folder structure
Graph
- nodes और edges का समूह
- उदाहरण: Google Maps या सोशल नेटवर्क

🔹 Common Algorithms:

Sorting – डेटा को क्रमबद्ध करना
- जैसे: Bubble Sort, Selection Sort, Merge Sort
Searching – किसी डेटा को ढूंढना
- जैसे: Linear Search, Binary Search
Recursion – जब कोई function खुद को call करता है
Dynamic Programming – जटिल समस्याओं को छोटे हिस्सों में बाँटना

** Data, Entity, Information, Difference between Data and Information, Data type ,Build in data type, Abstract data type, Definition of data structures, Types of Data Structures: Linear and Non-Linear Data Structure, Introduction to Algorithms: Definition of Algorithms, Difference between algorithm and programs, properties of algorithm, Algorithm Design Techniques, Performance Analysis of Algorithms, Complexity of various code structures, Order of Growth, Asymptotic Notations.

📘 Programming and Data Structures – Hinglish Notes

1. Data, Entity, Information

Data (डेटा): कच्चे तथ्य या आंकड़े जिनका कोई स्पष्ट अर्थ नहीं होता।
Entity (इकाई): कोई भी वस्तु जिसे पहचाना जा सके (जैसे student, car)।
Information (सूचना): जब डेटा को प्रोसेस कर लिया जाता है ताकि वह उपयोगी बन सके।

2. Difference between Data and Information

Data बिना प्रोसेस किया गया तथ्य होता है।
Information प्रोसेस किए गए डेटा से प्राप्त अर्थपूर्ण नतीजा होता है।

3. Data Type (डेटा प्रकार)

वह प्रकार जो किसी variable के डेटा को परिभाषित करता है।
उदहारण: int, float, char, bool

4. Built-in Data Types (इनबिल्ट डेटा टाइप्स)

जो डेटा टाइप्स language में पहले से मौजूद होते हैं।
उदाहरण: C में int, float, char

5. Abstract Data Type (ADT)

ADT (सारगर्भित डेटा प्रकार) एक logical model है कि डेटा को कैसे store और process किया जाए।
जैसे: Stack, Queue, List

6. Definition of Data Structures

डेटा को organize और store करने का तरीका ताकि उस पर operations efficiently perform किए जा सकें।

7. Types of Data Structures

👉 Linear & Non-Linear:

Linear (रेखीय): डेटा सीधी लाइन में होता है → Array, Stack, Queue, Linked List
Non-Linear (गैर-रेखीय): डेटा hierarchical या graph रूप में → Tree, Graph

8. Introduction to Algorithms

Algorithm (एल्गोरिदम) एक steps का set होता है जिससे कोई काम solve किया जाता है।

9. Definition of Algorithm

एक finite step-by-step procedure जो किसी समस्या का समाधान देता है।

10. Difference between Algorithm and Program

Algorithm logic को define करता है।
Program उस logic को किसी language में implement करता है।

11. Properties of Algorithm

Input
Output
Finiteness
Effectiveness
Definiteness

12. Algorithm Design Techniques

Divide and Conquer
Greedy
Dynamic Programming
Backtracking
Branch and Bound

13. Performance Analysis of Algorithms

Algorithm की efficiency को evaluate करना (Time और Space Complexity)

14. Complexity of Code Structures

Code में loops, recursion, आदि के आधार पर कितना समय या memory लगेगी।

15. Order of Growth

कैसे input size बढ़ने पर algorithm का समय बढ़ता है।
उदाहरण: O(1), O(n), O(n^2)

16. Asymptotic Notations

Algorithm के growth को represent करने के symbols:
- Big-O (O) → Worst Case
- Omega (Ω) → Best Case
- Theta (Θ) → Average Case

** Definition, Single and Multidimensional Arrays, Representation of Arrays: Row Major Order, and Column Major Order, Derivation of Index Formulae for 1-D,2-D Array Application of arrays, Sparse Matrices and their representations.
Recursion: recursion in C, example of recursion, Tower of Hanoi Problem, simulating recursion, Backtracking,, recursive algorithms, principles of
recursion.

🧮 Arrays (एरेज़)

🔹 Definition:

Array एक डेटा संरचना है जिसमें एक जैसे प्रकार के डेटा को क्रमबद्ध (sequence में) तरीके से स्टोर किया जाता है।

🔹 Types of Arrays:

Single Dimensional Array (एक-आयामी एरे):
जैसे – int arr[5] = {1, 2, 3, 4, 5};
Multidimensional Array (बहु-आयामी एरे):
जैसे – 2D array: int arr[2][3] = {{1,2,3},{4,5,6}};

🔹 Representation of Arrays:

Row Major Order (रो मेजर ऑर्डर):
डेटा को row by row memory में स्टोर किया जाता है।
Column Major Order (कॉलम मेजर ऑर्डर):
डेटा को column by column memory में स्टोर किया जाता है।

🔹 Index Formula (इंडेक्स सूत्र):

1-D Array:
Address = Base + (Index × Size of data type)
2-D Array:
- Row Major: Address = Base + [(i × No. of Columns) + j] × size
- Column Major: Address = Base + [(j × No. of Rows) + i] × size

🔹 Applications of Arrays (एरेज़ के उपयोग):

Searching & Sorting
Matrix Operations
Data Tables
Image processing (2D array)

🔹 Sparse Matrix (स्पार्स मैट्रिक्स):

ऐसी मैट्रिक्स जिसमें ज़्यादातर elements 0 होते हैं।
Memory बचाने के लिए sparse representation किया जाता है।

🔁 Recursion (रिकर्शन)

🔹 Definition:

जब कोई function खुद को call करता है, उसे recursion कहते हैं।

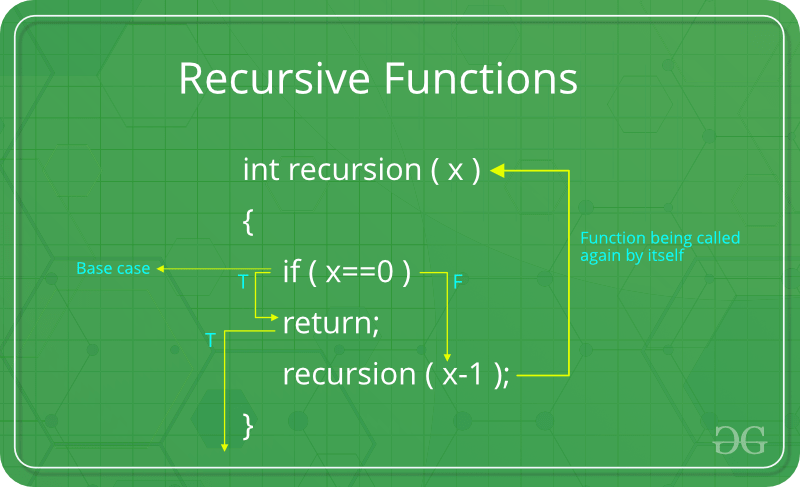
🔹 Topics:

Recursion in C
- जैसे factorial, Fibonacci series आदि को recursion से हल करना।
Example of Recursion int factorial(int n) { if (n == 0) return 1; else return n * factorial(n - 1); }
Tower of Hanoi Problem
- Classic recursive problem तीन pegs और कई disks के साथ।
Simulating Recursion
- Stack का उपयोग कर के recursion को iterative तरीके से simulate करना।
Backtracking (बैकट्रैकिंग)
- एक recursive तकनीक जिसमें हम गलत रास्ते से लौट कर सही रास्ता खोजते हैं।
- उदाहरण: N-Queens problem, Maze solving
Recursive Algorithms
- Algorithms जो recursion का उपयोग करते हैं जैसे Merge Sort, Quick Sort
Principles of Recursion
- Base Case
- Recursive Case
- Progress towards base case

** Array Implementation and Pointer Implementation of Singly Linked Lists, Doubly Linked List, Circularly Linked List, Operations on a Linked List.
Insertion, Deletion, Traversal, Polynomial Representation and Addition Subtraction & Multiplications of Single variable.

🔗 Linked Lists (लिंक्ड लिस्ट्स)

🔹 Array vs Pointer Implementation:

Array Implementation:
डेटा को लगातार memory blocks में स्टोर किया जाता है।
Pointer Implementation:
हर node में data और एक pointer होता है जो अगले node को point करता है।

🔹 Types of Linked Lists:

Singly Linked List (सिंगली लिंक्ड लिस्ट):
हर node में data और next pointer होता है।
👉 Traversal केवल एक दिशा में।
Doubly Linked List (डबल्ली लिंक्ड लिस्ट):
हर node में next और previous दो pointers होते हैं।
👉 Traversal दोनों दिशाओं में।
Circularly Linked List (सर्कुलर लिंक्ड लिस्ट):
लास्ट node का pointer first node को point करता है।
👉 List एक circle में घूमती है।

🔹 Operations on a Linked List (ऑपरेशंस):

Insertion (डाटा जोड़ना):
- Beginning, End, या किसी position पर
Deletion (डाटा हटाना):
- Specific node, first, या last node
Traversal (ट्रैवर्सल):
- एक-एक node पर जाकर पूरा list पढ़ना

🔹 Polynomial Representation using Linked List:

Polynomial जैसे 4x^3 + 3x^2 + x + 7 को linked list से represent किया जा सकता है।
हर node में coefficient और exponent होता है।

🔹 Polynomial Operations:

Addition (जोड़): दो polynomials के like terms को जोड़ना
Subtraction (घटाव): like terms को घटाना
Multiplication (गुणा): हर term को दूसरे polynomial की हर term से multiply करना

** Abstract Data Type, Primitive Stack operations: Push & Pop, Array and Linked Implementation of Stack in C, Application of stack: Prefix and Postfix Expressions, Evaluation of postfix expression, Iteration and Recursion Principles of recursion, Tail recursion, Removal of recursion Problem solving using iteration and recursion with examples such as binary search,
Fibonacci numbers, and Hanoi towers.

🥞 Stack (स्टैक)

🔹 Abstract Data Type (ADT):

Stack एक ADT है जिसमें डेटा Last In, First Out (LIFO) order में रखा जाता है।
👉 मतलब जो सबसे बाद में डाला जाता है, वही सबसे पहले निकलेगा।

🔹 Primitive Stack Operations:

Push (डाटा डालना)
– Stack में element जोड़ना।
Pop (डाटा निकालना)
– Stack से सबसे ऊपर का element हटाना।

🔹 Implementation in C:

Array Implementation:
- Stack को एक array की मदद से बनाया जाता है।
Linked List Implementation:
- हर node में data और next pointer होता है, जिससे dynamic size मिलती है।

🔹 Applications of Stack:

Prefix & Postfix Expressions (पूर्वसूचक और पश्चसूचक एक्सप्रेशन्स)
- Stack का उपयोग इन expressions को evaluate करने में होता है।
Evaluation of Postfix Expression:
- Expression जैसे 23*54*+9- को Stack से solve किया जाता है।

🔁 Recursion (रिकर्शन)

🔹 Iteration vs Recursion:

Iteration (पुनरावृत्ति): Loop जैसे for, while
Recursion: Function खुद को call करता है।

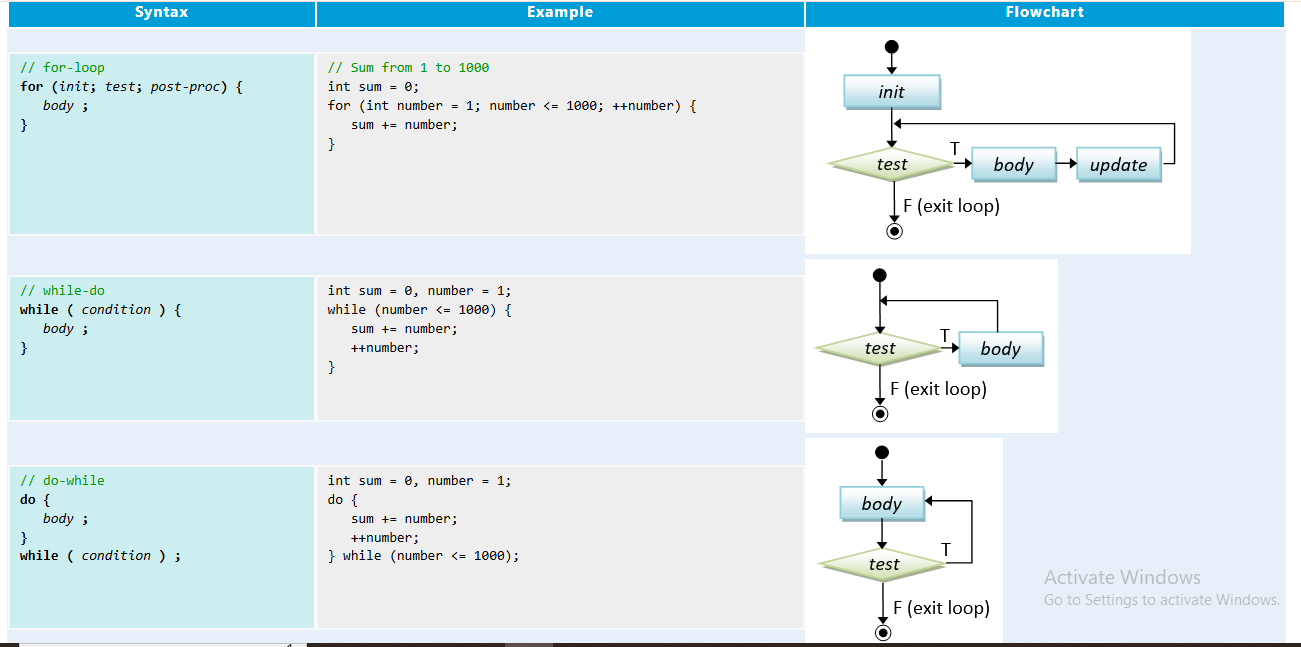
🔹 Principles of Recursion (रिकर्शन के सिद्धांत):

Base Case: कब रुकना है
Recursive Case: खुद को call करना
Progress: हर बार target के पास जाना

🔹 Tail Recursion (टेल रिकर्शन):

जब recursive call function के आखिरी में हो
Optimization के लिए useful होता है

🔹 Removal of Recursion Problem:

Recursion को iteration से replace करना
Stack का उपयोग करके recursion को simulate किया जा सकता है

🧠 Problem Solving Using Iteration and Recursion

Binary Search:
Recursion और iteration दोनों से implement किया जा सकता है।
🔍 Divide and Conquer algorithm
Fibonacci Numbers:
- Recursion: fib(n) = fib(n-1) + fib(n-2)
- Iteration: Loop से calculate किया जाता है
Tower of Hanoi:
Recursive method से solve किया जाता है।
👉 Classic example of recursion with 3 pegs and n disks.

Great! This image covers Queue and its operations. Here’s the full explanation in Hinglish (English + हिंदी में Devanagari script):

📥 Queue (क्यू)

Queue एक Linear Data Structure है जो FIFO (First In, First Out) principle पर काम करता है।
👉 जो item पहले डाला गया, वही पहले निकलेगा — जैसे टिकट की लाइन।

🔹 Operations on Queue:

Create (निर्माण):
नया empty queue बनाना।
Add / Enqueue (डालना):
Queue के पीछे नया element जोड़ना।
Delete / Dequeue (निकालना):
Queue के आगे से element हटाना।
Full (पूरा भरना):
जब queue में और element नहीं जोड़े जा सकते।
Empty (खाली):
जब queue में कोई भी element नहीं होता।

🔹 Types of Queues:

Linear Queue (रेखीय क्यू):
Simple queue जिसमें insertion पीछे से और deletion आगे से होता है।
Circular Queue (वृत्ताकार क्यू):
आखिरी position के बाद वापस पहले position पर insert किया जा सकता है।
👉 Space wastage को रोकता है।
Deque (Double Ended Queue):
इसमें insertion और deletion दोनों ends (front और rear) से हो सकता है।
Priority Queue (प्राथमिकता क्यू):
Element को उनकी priority के अनुसार process किया जाता है — ना कि arrival order के अनुसार।

🔹 Implementation in C:

Array Implementation:
- Fixed size का queue
- Static memory allocation
Linked List Implementation:
- Dynamically growing queue
- Front और rear pointers का इस्तेमाल होता है

🔚 Summary:

Queue = FIFO
Operations = Enqueue, Dequeue, Full/Empty Check
Types = Linear, Circular, Deque, Priority
Implementation = Array या Linked List

अगर आप चाहें तो मैं इन सभी queues के C language में कोड, diagrams, और dry run examples भी बना सकता हूँ। बताइए क्या चाहिए?

** Concept of Searching, Sequential search, Index Sequential Search, Binary Search. Concept of Hashing & Collision resolution Techniques used in Hashing.

1. खोज (Searching) का सिद्धान्त

खोज का अर्थ है किसी दिए गए तत्व (जिसे कुंजी या key कहते हैं) को किसी डाटा संरचना (जैसे सरणी, सूची, फ़ाइल, या डाटाबेस) में ढूँढना।

उद्देश्य → यह पता लगाना कि तत्व मौजूद है या नहीं, और यदि है तो कहाँ स्थित है।
मुख्य प्रकार:
1. क्रमिक खोज (Sequential) – एक-एक करके जाँचना।
2. सूचकांक/द्विआधारी/हैशिंग – सीधे या तेज़ी से सही स्थान पर पहुँचना।

2. क्रमिक खोज (Sequential Search / Linear Search)

प्रक्रिया → पहले तत्व से आरम्भ करके अंतिम तक प्रत्येक तत्व को कुंजी से मिलाया जाता है।
सर्वोत्तम स्थिति → पहला ही तत्व मिल जाए।
सबसे ख़राब स्थिति → अंतिम में मिले या बिल्कुल न मिले।
समय जटिलता →
- सर्वोत्तम: O(1)
- सबसे ख़राब: O(n)
लाभ → सरल, डाटा का क्रमबद्ध होना आवश्यक नहीं।
हानि → बड़े डाटा के लिए धीमी गति।

उदाहरण:

सरणी: [12, 45, 7, 33]
कुंजी: 33
जाँच: 12 → 45 → 7 → 33 → मिल गया, स्थान 4

3. सूचकांक क्रमिक खोज (Index Sequential Search)

विचार → बड़े डाटा को छोटे-छोटे खंडों में बाँटकर एक सूचकांक (index) बनाना, जिसमें प्रत्येक खंड का अधिकतम मान और उसका पता (pointer) रखा जाता है।
प्रक्रिया:
1. पहले सूचकांक सारणी में यह देखें कि कुंजी किस खंड में होगी।
2. उस खंड में क्रमिक खोज करें।
समय जटिलता → लगभग O(√n)।
उपयोग → डाटाबेस, बड़े फ़ाइल खोज कार्य।

4. द्विआधारी खोज (Binary Search)

शर्त → डाटा क्रमबद्ध (sorted) होना चाहिए।
कदम:
1. मध्य (middle) तत्व चुनें और कुंजी से तुलना करें।
2. यदि कुंजी = मध्य → मिल गया।
3. यदि कुंजी < मध्य → बाएँ हिस्से में खोजें।
4. यदि कुंजी > मध्य → दाएँ हिस्से में खोजें।
समय जटिलता → O(log₂ n)।
लाभ → बड़े क्रमबद्ध डाटा में बहुत तेज़।
हानि → डाटा को क्रमबद्ध रखना पड़ता है।

5. हैशिंग (Hashing) का सिद्धान्त

विचार → एक हैश फलन (hash function) का प्रयोग करके कुंजी का सीधे स्थान (index) निकालना, ताकि पूरे डाटा को न खंगालना पड़े।
लक्ष्य → औसतन O(1) समय में खोज।

उदाहरण:

हैश फलन: स्थान = कुंजी % 10
कुंजी: 27 → 27 % 10 = 7 → स्थान 7 पर संग्रहित/खोजें

6. टकराव (Collision)

परिभाषा → जब दो अलग-अलग कुंजियों का हैश पता (hash address) समान हो जाए।

उदाहरण:

27 % 10 = 7
37 % 10 = 7

दोनों स्थान 7 पर जाएँगे → टकराव।

7. टकराव निवारण विधियाँ (Collision Resolution Techniques)

(क) खुला संबोधन (Open Addressing)

यदि इच्छित स्थान भरा है तो तालिका में अगला रिक्त स्थान ढूँढें।
प्रकार:
1. रेखीय खोज (Linear Probing) → अगला, फिर अगला स्थान जाँचें।
2. वर्गात्मक खोज (Quadratic Probing) → दूरी 1², 2², 3²… पर जाँचें।
3. द्वि-हैशिंग (Double Hashing) → छलांग आकार के लिए दूसरा हैश फलन प्रयोग करें।

(ख) श्रंखला पद्धति (Chaining)

प्रत्येक स्थान पर एक लिंक्ड सूची रखी जाती है, जिसमें समान हैश मान वाले सभी तत्व संग्रहीत होते हैं।

(ग) पुनः हैशिंग (Rehashing)

जब लोड फैक्टर अधिक हो जाए, तो तालिका का आकार बढ़ाकर नये हैश पते निकाले जाते हैं।

** Insertion Sort, Selection Sort, Bubble Sort, Heap Sort, Comparison of Sorting Algorithms, Sorting in Linear Time: Counting Sort and Bucket Sort

ठीक है, अब मैं आपको यह पूरा Sorting का टॉपिक शुद्ध हिन्दी में लिखकर देता हूँ।

1. प्रविष्टि क्रम (Insertion Sort)

सिद्धान्त → एक-एक करके तत्वों को लिया जाता है और उन्हें पहले से क्रमबद्ध भाग में सही स्थान पर प्रविष्ट किया जाता है (जैसे हम ताश के पत्तों को क्रमबद्ध करते हैं)।

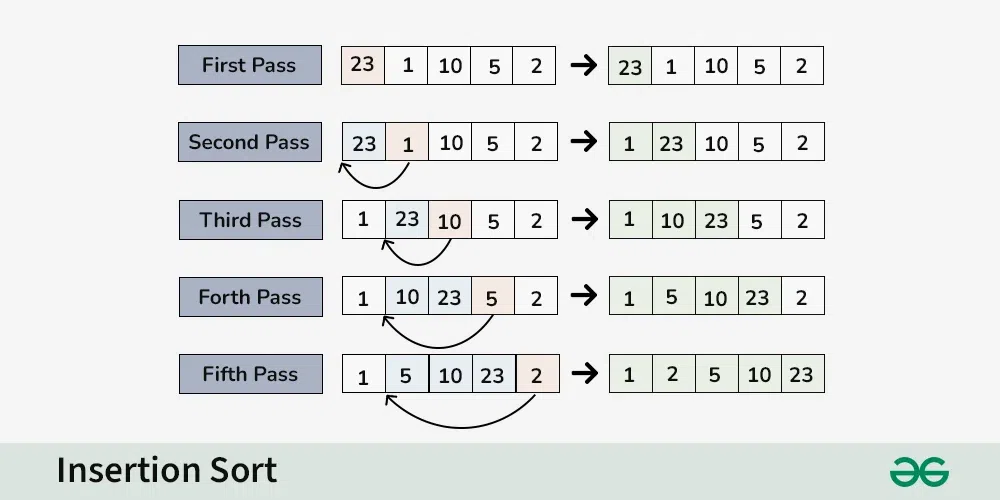
चरण:

पहले तत्व को क्रमबद्ध मान लें।
अगला तत्व लें और उसे क्रमबद्ध भाग में उचित स्थान पर प्रविष्ट करें (इसके लिए कुछ तत्वों को आगे खिसकाना पड़ सकता है)।
यह प्रक्रिया तब तक दोहराएँ जब तक सभी तत्व क्रमबद्ध न हो जाएँ।

समय जटिलता →
- सर्वोत्तम: O(n) (यदि सूची पहले से क्रमबद्ध हो)
- सबसे ख़राब: O(n²)
स्थान → O(1) (इन-प्लेस)
स्थिरता → हाँ

2. चयन क्रम (Selection Sort)

सिद्धान्त → प्रत्येक बार सबसे छोटा तत्व ढूँढकर उसे सही स्थान पर रख देना।

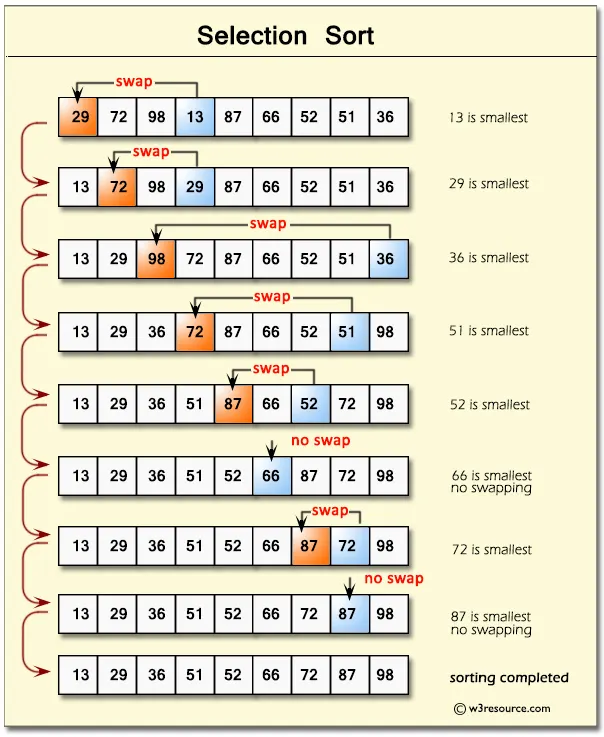
चरण:

पूरी सरणी में सबसे छोटा तत्व ढूँढें और उसे प्रथम स्थान के तत्व से अदला-बदली करें।
दूसरे स्थान से पुनः सबसे छोटा तत्व ढूँढें और अदला-बदली करें।
इसी प्रकार पूरी सूची को क्रमबद्ध करें।

समय जटिलता → सदैव O(n²)
स्थान → O(1)
स्थिरता → नहीं

3. बुलबुला क्रम (Bubble Sort)

सिद्धान्त → बार-बार पास-पास के तत्वों की तुलना करना और यदि वे गलत क्रम में हैं तो उनकी अदला-बदली करना (बड़े तत्व ऊपर “बुलबुला” की तरह आ जाते हैं)।

चरण:

पहले तत्व से तुलना आरम्भ करें, अगले से मिलाएँ।
यदि क्रम गलत है तो अदला-बदली करें।
एक चक्र पूरा होने पर सबसे बड़ा तत्व सूची के अंत में पहुँच जाएगा।
शेष सूची के लिए प्रक्रिया दोहराएँ।

समय जटिलता →
- सर्वोत्तम: O(n) (यदि पहले से क्रमबद्ध हो और अनुकूलित संस्करण हो)
- सबसे ख़राब: O(n²)
स्थान → O(1)
स्थिरता → हाँ

4. ढेर क्रम (Heap Sort)

सिद्धान्त → अधिकतम-ढेर (Max-Heap) संरचना बनाकर सबसे बड़े तत्व को बार-बार निकालना।

चरण:

सरणी को अधिकतम-ढेर में बदलें।
मूल (root) तत्व को अंतिम तत्व से अदला-बदली करें, ढेर का आकार 1 घटाएँ।
पुनः ढेर को व्यवस्थित करें (heapify)।
तब तक दोहराएँ जब तक सभी तत्व क्रमबद्ध न हो जाएँ।

समय जटिलता → सदैव O(n log n)
स्थान → O(1)
स्थिरता → नहीं

5. क्रमण विधियों की तुलना

क्रमण विधि	सर्वोत्तम समय	सबसे ख़राब समय	स्थान	स्थिरता	टिप्पणी
प्रविष्टि क्रम	O(n)	O(n²)	O(1)	हाँ	छोटे डाटा के लिए अच्छा
चयन क्रम	O(n²)	O(n²)	O(1)	नहीं	न्यूनतम अदला-बदली, पर धीमा
बुलबुला क्रम	O(n)	O(n²)	O(1)	हाँ	सरल, पर व्यवहार में कम
ढेर क्रम	O(n log n)	O(n log n)	O(1)	नहीं	बड़े डाटा के लिए उपयुक्त

6. रैखिक समय में क्रमण (Sorting in Linear Time)

(क) गणना क्रम (Counting Sort)

सिद्धान्त → प्रत्येक तत्व की आवृत्ति (frequency) गिनना और फिर संचयी योग से सही स्थान निर्धारित करना।
केवल ज्ञात सीमा (range) वाले पूर्णांकों के लिए उपयुक्त।

चरण:

सीमा के अनुसार गणना-सरणी (count array) बनाएँ।
प्रत्येक तत्व की संख्या गिनें।
संचयी योग (prefix sum) लें → स्थान प्राप्त होंगे।
परिणाम-सरणी में तत्व रखें।

समय जटिलता → O(n + k), जहाँ k = सीमा का आकार
स्थिरता → हाँ

(ख) बाल्टी क्रम (Bucket Sort)

सिद्धान्त → मानों (values) को अलग-अलग “बाल्टियों” में बाँटना, प्रत्येक बाल्टी को क्रमबद्ध करना, और फिर सभी को जोड़ देना।
समान वितरण (uniform distribution) वाले सतत डाटा के लिए अच्छा।

चरण:

सीमा के अनुसार बाल्टियाँ बनाएँ।
तत्वों को उनकी बाल्टी में डालें।
प्रत्येक बाल्टी को क्रमबद्ध करें (जैसे प्रविष्टि क्रम से)।
सभी बाल्टियों को जोड़ दें।

समय जटिलता → औसत O(n + k), k = बाल्टियों की संख्या
स्थिरता → इस पर निर्भर करता है कि बाल्टी के भीतर कौन-सी विधि प्रयोग की गई है।

अगर आप चाहें तो मैं इन सभी Sorting Algorithms के चित्र (diagrams) और चरण-दर-चरण सूखी रनिंग (dry run) उदाहरण भी बना सकता हूँ, जिससे ये और स्पष्ट हो जाएँ।
क्या आप चाहते हैं कि मैं वो बना दूँ?

** Terminology used with Graph, Data Structure for Graph Representations: Adjacency Matrices, Adjacency List, Adjacency. Graph Traversal: Depth First Search and Breadth First Search, Connected Component.

1. ग्राफ से जुड़ी पारिभाषिक शब्दावली (Terminology used with Graph)

शीर्ष / नोड (Vertex / Node) – ग्राफ का एक बिंदु, जहाँ से रेखाएँ (edges) जुड़ती हैं।
धनु / धार (Edge) – दो शीर्षों के बीच का संबंध या रेखा।
सन्निकट शीर्ष (Adjacent Vertices) – ऐसे दो शीर्ष जिनके बीच प्रत्यक्ष धार हो।
डिग्री (Degree) – किसी शीर्ष से जुड़ी धारों की संख्या।
- In-degree – किसी शीर्ष पर आने वाली धारों की संख्या।
- Out-degree – किसी शीर्ष से जाने वाली धारों की संख्या।
पथ (Path) – शीर्षों और धारों का क्रमबद्ध अनुक्रम।
चक्र (Cycle) – ऐसा पथ जो एक ही शीर्ष से प्रारम्भ होकर उसी पर समाप्त हो और बीच में कोई शीर्ष दोहराया न जाए।
सरल ग्राफ (Simple Graph) – जिसमें कोई self-loop और parallel edge न हो।
वजनित ग्राफ (Weighted Graph) – जिसमें धारों के साथ भार (weight) जुड़ा हो।
संपर्कित ग्राफ (Connected Graph) – जिसमें हर शीर्ष दूसरे शीर्ष से किसी पथ द्वारा जुड़ा हो।

2. ग्राफ के निरूपण के लिए डाटा संरचनाएँ (Data Structure for Graph Representation)

(क) सन्निकटता मैट्रिक्स (Adjacency Matrix)

एक n × n का द्विविमीय सरणी (matrix), जहाँ n = शीर्षों की संख्या।
यदि शीर्ष i और j के बीच धार है → matrix[i][j] = 1 (या weight)।
यदि धार नहीं है → matrix[i][j] = 0।
लाभ → धार की उपस्थिति जाँचने में O(1) समय।
हानि → स्थान जटिलता O(n²), sparse graph में space की बर्बादी।

(ख) सन्निकटता सूची (Adjacency List)

प्रत्येक शीर्ष के लिए एक सूची बनाई जाती है जिसमें उसके सभी सन्निकट शीर्षों का विवरण होता है।
लाभ → Sparse graph के लिए space-efficient (O(V + E))।
हानि → किसी विशेष edge की उपस्थिति ढूँढना O(degree) समय ले सकता है।

(ग) सन्निकटता बहु-सूची (Adjacency Multilist)

विशेष रूप से undirected graphs के लिए, जहाँ हर धार को केवल एक बार store करने के लिए संरचना बनाई जाती है।
हर edge node में दोनों endpoints की जानकारी और pointers रहते हैं।
उपयोग → बड़ी और जटिल graph operations में।

3. ग्राफ का परिभ्रमण (Graph Traversal)

Traversal का अर्थ है सभी शीर्षों को किसी क्रम से विज़िट करना।

(क) गहराई-प्रथम खोज (Depth First Search – DFS)

विचार → जितना संभव हो उतना गहराई में जाएँ, फिर वापस लौटें।
प्रक्रिया:
1. प्रारम्भिक शीर्ष से शुरू करें।
2. उसे visit करें और उसे visited चिह्नित करें।
3. किसी unvisited सन्निकट शीर्ष पर जाएँ और यही प्रक्रिया दोहराएँ।
4. जब कोई unvisited शीर्ष न मिले, पीछे लौटें।
उपयोग → Topological sort, connected components, cycle detection।

(ख) चौड़ाई-प्रथम खोज (Breadth First Search – BFS)

विचार → पहले वर्तमान स्तर के सभी शीर्ष विज़िट करें, फिर अगले स्तर पर जाएँ।
प्रक्रिया:
1. प्रारम्भिक शीर्ष से शुरू करें।
2. उसे queue में डालें और visited करें।
3. Queue से एक शीर्ष निकालें, उसके सभी unvisited सन्निकट शीर्ष queue में डालें।
4. जब तक queue खाली न हो, प्रक्रिया दोहराएँ।
उपयोग → Shortest path (unweighted graph), level order traversal।

4. संपर्कित घटक (Connected Component)

परिभाषा → ग्राफ का वह उप-ग्राफ जिसमें सभी शीर्ष एक-दूसरे से जुड़े हों और बाहर के किसी शीर्ष से जुड़ाव न हो।
किसी undirected graph में connected components DFS या BFS से निकाले जा सकते हैं।
यदि ग्राफ connected है → केवल एक connected component होगा।

** Basic terminology used with Tree, Binary Trees, Binary Tree Representation: Array Representation and Pointer (Linked List) Representation, Binary Search Tree, Complete Binary Tree, A Extended Binary Trees, Tree Traversal algorithms: Inorder, Preorder and Postorder, Constructing Binary Tree from
given Tree Traversal, Operation of Insertion, Deletion, Searching & Modification of data in Binary Search Tree. Threaded Binary trees, Huffman coding using Binary Tree, AVL Tree and B Tree

1. ट्री से संबंधित मूल शब्दावली (Basic Terminology used with Tree)

Node (नोड): डाटा रखने का एक बिंदु।
Root (जड़): ट्री का सबसे ऊपरी नोड।
Edge (किनारा): दो नोड को जोड़ने वाली रेखा।
Parent (जनक): कोई नोड जिसके नीचे चाइल्ड हो।
Child (संतान): किसी नोड के नीचे जुड़ा नोड।
Leaf (पत्ती): जिसके कोई चाइल्ड नहीं हैं।
Height (ऊँचाई): Root से सबसे गहरे नोड तक की लंबाई।
Depth (गहराई): Root से किसी नोड तक का रास्ता।
Sibling (सहोदर): एक ही Parent के अलग-अलग बच्चे।

2. बाइनरी ट्री (Binary Tree)

परिभाषा:
एक ऐसा ट्री जिसमें प्रत्येक नोड के अधिकतम दो बच्चे हो सकते हैं – Left Child और Right Child।

3. बाइनरी ट्री का निरूपण (Binary Tree Representation)

(A) Array Representation

Root को index 1 (या 0) पर रखते हैं।
अगर किसी नोड का index i है:
- Left Child = index 2i
- Right Child = index 2i + 1

समस्या: Sparse (खाली जगह वाले) ट्री में Memory Waste होती है।

(B) Pointer (Linked List) Representation

हर नोड के पास तीन हिस्से:
1. Data
2. Left Child का Pointer
3. Right Child का Pointer

4. बाइनरी सर्च ट्री (BST – Binary Search Tree)

नियम:

बाएं subtree के सभी नोड का मान root से छोटा हो।
दाएं subtree के सभी नोड का मान root से बड़ा हो।

5. Complete Binary Tree (पूर्ण बाइनरी ट्री)

सभी Level पूरी तरह भरे हों, और अंतिम Level के नोड बाएं से दाएं भरे जाएं।

6. Extended Binary Tree (विस्तारित बाइनरी ट्री)

NULL pointers को भी एक special External Node से बदल दिया जाता है।

7. Tree Traversal Algorithms (ट्री का भ्रमण)

Inorder (Left → Root → Right)
Preorder (Root → Left → Right)
Postorder (Left → Right → Root)

8. Constructing Binary Tree from Traversals

अगर Inorder + Preorder दिए हों → ट्री बनाया जा सकता है।
अगर Inorder + Postorder दिए हों → ट्री बनाया जा सकता है।

9. BST में ऑपरेशन्स

Insertion (प्रवेश): नए नोड को नियम के अनुसार डालना।
Deletion (हटाना): तीन केस होते हैं –
1. Leaf Node हटाना।
2. Single Child वाला Node हटाना।
3. दो बच्चों वाला Node (Inorder Successor या Predecessor से बदलना)।
Searching (खोजना): Root से शुरू करके Left या Right में देखना।
Modification (संशोधन): Node के Data को बदलना।

10. Threaded Binary Tree

NULL Pointers की जगह Traversal में अगले नोड का Pointer रख देते हैं ताकि Inorder traversal बिना Recursion/Stack के हो सके।

11. Huffman Coding using Binary Tree

Character frequencies के आधार पर एक Binary Tree बनाया जाता है।
Left edge को 0 और Right edge को 1 देते हैं।
कम लंबाई के कोड अधिक frequency वाले characters को मिलते हैं।

12. AVL Tree (Self-Balancing BST)

हर नोड का Balance Factor = Height(Left) – Height(Right) होता है।
यह हमेशा -1, 0, 1 में से एक होना चाहिए।
अगर नहीं है, तो Rotations करके संतुलित करते हैं (LL, RR, LR, RL)।

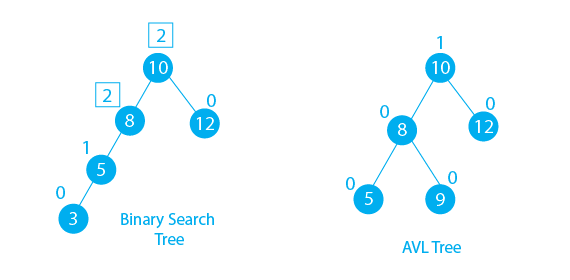
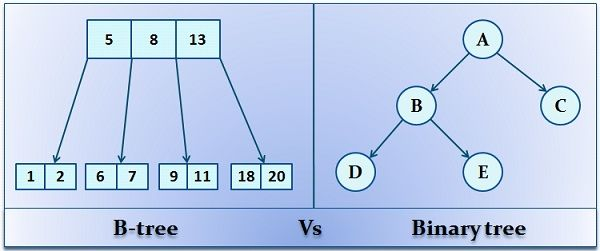
13. B Tree

Disk storage के लिए उपयोग किया जाने वाला self-balancing search tree।
एक नोड में कई Keys हो सकती हैं।
Binary Tree के बजाय B-Tree बड़े blocks में डेटा store करता है।

References:

1.https://www3.ntu.edu.sg/home/ehchua/programming/index.html

** Introduction **

🔹 Programming क्या होता है?

🧠 Basic Concepts:

🔹 Data Structures क्या होते हैं?

📚 मुख्य Data Structures:

🔹 Common Algorithms:

📘 Programming and Data Structures – Hinglish Notes

1. Data, Entity, Information

2. Difference between Data and Information

3. Data Type (डेटा प्रकार)

4. Built-in Data Types (इनबिल्ट डेटा टाइप्स)

5. Abstract Data Type (ADT)

6. Definition of Data Structures

7. Types of Data Structures

👉 Linear & Non-Linear:

8. Introduction to Algorithms

9. Definition of Algorithm

10. Difference between Algorithm and Program

11. Properties of Algorithm

12. Algorithm Design Techniques

13. Performance Analysis of Algorithms

14. Complexity of Code Structures

15. Order of Growth

16. Asymptotic Notations

🧮 Arrays (एरेज़)

🔹 Definition:

🔹 Types of Arrays:

🔹 Representation of Arrays:

🔹 Index Formula (इंडेक्स सूत्र):

🔹 Applications of Arrays (एरेज़ के उपयोग):

🔹 Sparse Matrix (स्पार्स मैट्रिक्स):

🔁 Recursion (रिकर्शन)

🔹 Definition:

🔹 Topics:

** Array Implementation and Pointer Implementation of Singly Linked Lists, Doubly Linked List, Circularly Linked List, Operations on a Linked List.Insertion, Deletion, Traversal, Polynomial Representation and Addition Subtraction & Multiplications of Single variable.

🔗 Linked Lists (लिंक्ड लिस्ट्स)

🔹 Array vs Pointer Implementation:

🔹 Types of Linked Lists:

🔹 Operations on a Linked List (ऑपरेशंस):

🔹 Polynomial Representation using Linked List:

🔹 Polynomial Operations:

🥞 Stack (स्टैक)

🔹 Abstract Data Type (ADT):

🔹 Primitive Stack Operations:

🔹 Implementation in C:

🔹 Applications of Stack:

🔁 Recursion (रिकर्शन)

🔹 Iteration vs Recursion:

🔹 Principles of Recursion (रिकर्शन के सिद्धांत):

🔹 Tail Recursion (टेल रिकर्शन):

🔹 Removal of Recursion Problem:

🧠 Problem Solving Using Iteration and Recursion

📥 Queue (क्यू)

🔹 Operations on Queue:

🔹 Types of Queues:

🔹 Implementation in C:

🔚 Summary:

** Concept of Searching, Sequential search, Index Sequential Search, Binary Search. Concept of Hashing & Collision resolution Techniques used in Hashing.

1. खोज (Searching) का सिद्धान्त

2. क्रमिक खोज (Sequential Search / Linear Search)

3. सूचकांक क्रमिक खोज (Index Sequential Search)

4. द्विआधारी खोज (Binary Search)

5. हैशिंग (Hashing) का सिद्धान्त

6. टकराव (Collision)

7. टकराव निवारण विधियाँ (Collision Resolution Techniques)

(क) खुला संबोधन (Open Addressing)

(ख) श्रंखला पद्धति (Chaining)

(ग) पुनः हैशिंग (Rehashing)

** Insertion Sort, Selection Sort, Bubble Sort, Heap Sort, Comparison of Sorting Algorithms, Sorting in Linear Time: Counting Sort and Bucket Sort

1. प्रविष्टि क्रम (Insertion Sort)

2. चयन क्रम (Selection Sort)

3. बुलबुला क्रम (Bubble Sort)

4. ढेर क्रम (Heap Sort)

5. क्रमण विधियों की तुलना

6. रैखिक समय में क्रमण (Sorting in Linear Time)

(क) गणना क्रम (Counting Sort)

(ख) बाल्टी क्रम (Bucket Sort)

** Terminology used with Graph, Data Structure for Graph Representations: Adjacency Matrices, Adjacency List, Adjacency. Graph Traversal: Depth First Search and Breadth First Search, Connected Component.

1. ग्राफ से जुड़ी पारिभाषिक शब्दावली (Terminology used with Graph)

2. ग्राफ के निरूपण के लिए डाटा संरचनाएँ (Data Structure for Graph Representation)

Introduction

** Array Implementation and Pointer Implementation of Singly Linked Lists, Doubly Linked List, Circularly Linked List, Operations on a Linked List.
Insertion, Deletion, Traversal, Polynomial Representation and Addition Subtraction & Multiplications of Single variable.